SIMPLIFYING SQUARE ROOTS

Problem 1:

√36

Solution:

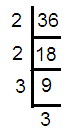√36 = √ (2∙2∙3∙3) For every two same values, take one value out of the radical. √36 = (2∙3) √36 = 6

Problem 2 :

√4

Solution :

√4 = √(2.2)

For every two same values, take one value out of the radical.

√4 = 2

Problem 3 :

√64

Solution :

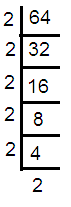√64 = √ (2∙2∙2∙2∙2∙2) For every two same values, take one value out of the radical. √64 = (2∙2∙2) √64 = 8

Problem 4 :

√144

Solution :

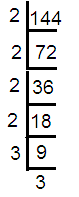√144 = √ (2∙2∙2∙2∙3∙3) For every two same values, take one value out of the radical. √144 = (2∙2∙3) √144 = 12

√144 = 12

Problem 5 :

- √4

Solution :

-√4 = -√ (2.2)

For every two same values, take one value out of the radical.

-√4 = - 2

Problem 6 :

-√100

Solution :

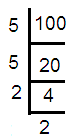-√100 = -√(5∙5∙2∙2) For every two same values, take one value out of the radical. -√100 = - (5∙2) -√100 = - 10

Problem 7 :

-√1

Solution :

-√1 = -1

Problem 8 :

-√121

Solution :

-√121 = -√ (11∙11)

For every two same values, take one value out of the radical.

-√121 = -11

Problem 9 :

√-36

Solution :

Since we have negative sign inside the radical sign, there is no real roots.

Problem 10 :

√-9

Solution :

Since we have negative sign inside the radical sign, there is no real roots.

Problem 11 :

√-49

Solution :

Since we have negative sign inside the radical sign, there is no real roots.

Problem 12:

√(9 + 16)

Solution:

√(9 + 16) = √25

√25 = √ (5∙5)

For every two same values, take one value out of the radical.

√25 = 5

Problem 13:

√25 + 144

Solution:

√25 + 144 = √169

√169 = √ (13∙13)

For every two same values, take one value out of the radical.

√169 = 13

Problem 14 :

√9 + √16

Solution :

√9 = √(3∙3)

√16 = √(2∙2∙2∙2) = 2 ∙ 2 ==> 4

For every two same values, take one value out of the radical.

√9 = 3

√16 = 4

√9 + √16 = 3 + 4

√9 + √16 = 7

Problem 15 :

√25 + √144

Solution:

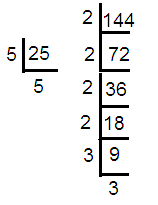√25 = √ (5∙5) √25 = 5 √144 = √ (2∙2∙2∙2∙3∙3) √144 = (2∙2∙3) √144 = 12 √25 + √144 = 5 + 12 √25 + √144 = 17

Problem 16 :

Find the square root of 6400

Solution :

√6400 = √ (2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 10 ∙ 10)

= 2 ∙ 2 ∙ 2 ∙ 10

= 80

So, the square root of 6400 is 80.

Problem 17 :

Is 2352 a perfect square? If not find the smallest multiple of 2352 which is a perfect square. Find the sqaure root of the new number.

Solution :

To check the given number is a perfect square or not, we have to decompose the number using prime factorization.

2352 = 2 x 2 x 2 x 2 x 3 x 7 x 7

3 is the smallest multiple should be removed to make it as perfect square.

= √ (2 ∙ 2 ∙ 2 ∙ 2 ∙ 7 ∙ 7)

= 2 ∙ 2 ∙ 7

= 28

Problem 18 :

2116 plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of rows and the number of plants in each row.

Solution :

Let x be the number of rows and columns.

x ∙ x = 2116

x² = 2116

x = √2116

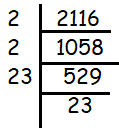
= √(2 ∙ 2 ∙ 23 ∙ 23)

= 2 ∙ 23

= 46

So, the number of rows and number of columns is 46.

Problem 19 :

A natural number is called a _________ or _____________ if it is the square of some natural numbers 

Solution :

A natural number is called a perfect square or square of number. if it is the square of some natural numbers.

Problem 20 :

Simplify √0.09

Solution :

= √0.09

= √0.09 x (100/100)

= √(9/100)

= √ (3 x 3) / (10 x 10)

= 3/10

= 0.3

Problem 21 :

Find the length of the side of a square whose area is 441 m²

Solution :

Area of square = 441 m²

Let x be the side length of square.

x ∙ x = √ 441

x ∙ x = √ (3 ∙ 7 ∙ 3 ∙ 7)

x = 3 ∙ 7

x = 21

So, the side length of square is 21 m.