SIMPLIFYING RATIONAL EXPRESSIONS

Simplify the rational expressions.

Example 1 :

(2x + 6) / (4x - 12)

Solution :

Example 2 :

(x² + 9x + 20) / (2x + 8)

Solution :

Example 3 :

(6x + 24)/(x² +7x + 12)

Solution :

Example 4 :

(3x + 18)/(x²+6x)

Solution :

Example 5 :

(3x - 12)/(3x² - 12x)

Solution :

Example 6 :

(x² - 5x + 6)/(x² + 2x - 15)

Solution :

Example 7 :

(4x + 4)/(x² + 4x + 3)

Solution :

Example 8 :

(x² - x - 12)/(x² - 2x - 8)

Solution :

Example 9 :

(x² - 5x + 4)/(x² - 4x)

Solution :

Example 10 :

(x² - x - 30)/(x² - 12x + 36)

Solution :

Write and simplify a rational expression for the ratio of the perimeter of the figure to its area.

Example 11 :

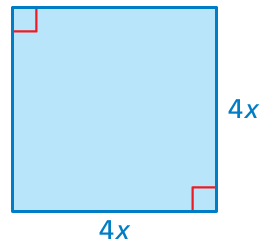
Solution :

Perimeter of square = 4(4x)

= 16x

Area of square = (4x)²

= 16x²

Ratio between perimeter to area = 16x : 16x²

= 16x/16x² 

= 1/x

So, the required ratio is 1 : x.

Example 12 :

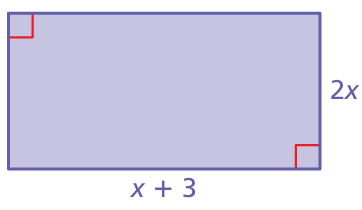
Solution :

Perimeter of rectangle = 2(x + 3 + 2x)

= 2(3x + 3)

Area of rectangle = (x + 3)2x

Ratio between perimeter and area = 2(3x + 3) : 2x(x + 3)

= 2(3x + 3) / 2x(x + 3)

= (3x + 3) / x(x + 3)

= (3x + 3) / (x² + 3x)

So, the required ratio is (3x + 3) : (x² + 3x)

Example 13 :

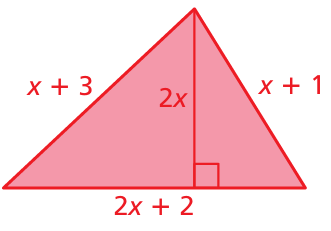
Solution :

Perimeter of triangle = 2x + 2 + x + 3 + x + 1

= 4x + 6

= 2(2x + 3)

Area of triangle = (1/2) ⋅ base ⋅ height

= (1/2) ⋅ (2x + 2) ⋅2x

= 2x (x + 1)

Ratio between perimeter ot area = 2(2x + 3) : 2x (x + 1)

= 2(2x + 3) / 2x (x + 1)

= (2x + 3) / x(x + 1)