SIMPLIFYING RATIONAL EXPONENTS

If we have power raised to another power, we have to multiply the powers.

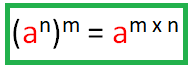
If we have numerical values inside the parenthesis,

• Decompose it as much as possible
• Write it in exponential form
• Then multiply the powers for further simplification.

Simplify the following without using calculator.

Example 1 :

(-32)^2/5

Solution :

= (-32)^2/5

Decomposing 32, we get

-32 = (-2) ⋅ (-2) ⋅ (-2) ⋅ (-2) ⋅ (-2)

-32 = (-2)⁵

(-32)^2/5  = [(-2)⁵]^2/5

Since we have power raised to another power, we have to multiply the powers.

= (-2)^5 ⋅ 2/5

= (-2)²

(-32)^2/5 = 4

Example 2 :

(-8)^4/3

Solution :

= (-8)^4/3

Decomposing -8, we get

-8 = (-2) ⋅ (-2) ⋅ (-2)

-8 = (-2)³

(-8)^4/3  = [(-2)³]^4/3

= (-2)³

= -8

Example 3 :

(8/27)^4/3

Solution :

= (8/27)^4/3

Decomposing 8 and 27, we get

(8/27)^4/3 = [(2/3)³]^4/3

= (2/3) ^{3 ⋅ (4/3)}

= (2/3)⁴

= 16/81

Example 4 :

(125)^1/3

Solution :

= (125)^1/3

Decomposing 125, we get

125 = 5 ⋅ 5 ⋅ 5 ==> 5³

= (5³)^1/3

= 5^{3 ⋅ (1/3)}

= 5

Example 5 :

(8x¹⁵)^-1/3

Solution :

= (8x¹⁵)^-1/3

Decomposing 8, we get

8 = 2 ⋅ 2 ⋅ 2 ==> 2³

= (2³ (x⁵)³)^-1/3

= (2x⁵)^{3 ⋅ (-1/3)}

= (2x⁵)^-1

=1/(2x⁵)

Example 6 :

(h⁶p⁹/1000m³)^-2/3

Solution :

Example 7 :

(64)^1/6

Solution :

= (64)^1/6

Decomposing 64, we get

64 = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2

64 = 2⁶

(64)^1/6 = (2⁶)^1/6

= 2 ^{(6 ⋅ 1/6)}

= 2

Example 8 :

(256)^3/4

Solution :

= (256)^3/4

Decomposing 256, we get

256 = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2

256 = 4⁴

(256)^3/4 = (4⁴)^3/4

= 4³

= 64

Example 8 :

evaluate the expression without using a calculator.

Solution :

a)  64^1/6

Step 1 :

Writing 64 in expanded form.

64 = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2

Step 2 :

Writing the expanded form in exponential form, we get

= 2⁶

Step 3 :

Replacing the exponential form in the question and multiplying the power raised by another power.

64^1/6 = (2⁶)^1/6

= 2^{6 x (1/6)}

= 2

b) 8^1/3

Step 1 :

Writing 8 in expanded form.

8 = 2 ⋅ 2 ⋅ 2 

Step 2 :

Writing the expanded form in exponential form, we get

= 2³

8^1/3 = (2³)^1/3 

= 2^3x(1/3)

= 2

c) 25^3/2

25 = 5 ⋅ 5

= 5²

25^3/2 = (5²)^3/2 

= 5^{2 x (3/2)}

= 5³

= 125

d) 81^3/4

Step 1 :

Writing 81 in expanded form.

81 = 9 ⋅ 9

Step 2 :

Writing the expanded form in exponential form, we get

= 3⁴

81^3/4 = (9²)^3/4 

= 9^{2 x (3/2)}

= 9³

= 729

e)  (−243)^1/5

Step 1 :

Writing 243 in expanded form.

243 = 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3

Step 2 :

Writing the expanded form in exponential form, we get

= 3⁵

(−243)^1/5 = ((-3)⁵)^1/5

= (-3)^{5 x (1/5)}

= -3

f)  (−64)^4/3

Step 1 :

Writing 64 in expanded form.

64 = 4 ⋅ 4 ⋅ 4

Step 2 :

Writing the expanded form in exponential form, we get

= 4³

(−64)^4/3 = ((-4)³)^4/3

= (-4)^{3 x (4/3)}

= (-4)⁴

We have negative base and even number as exponent, then the negative sign can be changes as positive.

= 256

g) 8^−2/3

8 = 2 ⋅ 2 ⋅ 2 ==> 8³

8^−2/3 = (8³)^−2/3

= 8⁻²

= 1/8²

= 1/64

h) 16^−7/4

16 = 2 ⋅ 2 ⋅ 2 ⋅ 2 ==> 2⁴

16^−7/4 = (2⁴)^−7/4

= 2⁻⁷

= 1/2⁷

= 1/128

Example 9 :

a)  3(11^11/4) + 9(11^11/4)

b)  13(8^3/4) − 4(8^3/4)

c)  27√6 + 7√150

d)  ∜(1296/25)

Solution :

a)  3(11^11/4) + 9(11^11/4)

Since these two are like terms, we can add them.

= 12(11^11/4)

It cannot be simplified further.

b)  13(8^3/4) − 4(8^3/4)

= 9(8^3/4)

= 9((2³)^3/4)

= 9(2^9/4)

c)  27√6 + 7√150

√150 = √(5 ⋅ 5 ⋅ 3 ⋅ 2)

= 5√6

27√6 + 7√150 = 27√6 + 5√6

= 33√6

d)  ∜(1296/625)

1296 = 6 ⋅ 6 ⋅ 6 ⋅ 6 ==> 6⁴

625 = 5 ⋅ 5 ⋅ 5 ⋅ 5 ==> 5⁴

∜(1296/625) = ∜(6⁴/5⁴)

= ∜(6/5)⁴

= 6/5

Example 10 :

Perform the indicated operation. Assume all variables are positive. 

a)  12 ∛y + 9 ∛y

b)  11 √2z − 5√2z

c) 3x^7/2− 5x^7/2

d) 7 ∛m⁷ + 3m^7/3

Solution :

a)  12 ∛y + 9 ∛y

= 21∛y

b)  11 √2z − 5√2z

= 6√2z

c) 3x^7/2− 5x^7/2

= -2 x^7/2

d) 7 ∛m⁷ + 3m^7/3

= 7 ∛m⁷ + 3m^7x(1/3)

= 7 ∛m⁷ + 3 ∛m⁷

= 10∛m⁷

Example 11 :

Perform the indicated operation. Assume all variables are positive. 

a) 125^4/3

b)  32^4/5

c) 625^3/4

d) 49^3/2

Solution :

a) 125^4/3

= (5³)^(4/3)

= 5^{3 x (4/3)}

= 5⁴

= 625

b)  32^4/5

= (2⁵)^(4/5)

= 2^{5 x (4/5)}

= 2⁴

= 16

c) 625^3/4

= (5⁴)^(3/4)

= 5^{4 x (3/4)}

= 5³

= 125

d) 49^3/2

= (7²)^(3/2)

= 7^{2 x (3/2)}

= 7³

= 343