SIMPLIFYING EXPRESSIONS WITH RATIONAL EXPONENTS

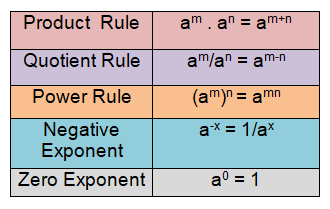
Using the properties of exponents, we  can simplify expressions with rational exponents.

Apply the properties of integer exponents to rational exponents by simplifying each expression.

Problem 1 :

5^2/3 ⋅ 5^4/3

Solution :

= 5^2/3 ⋅ 5^4/3

Here two terms are having same base, so we can put only one power and add the exponents.

= 5^{(2/3 + 4/3)}

= 5^(2+4)/3

= 5^6/3

= 5²

5^2/3 ⋅ 5^4/3 = 25

Problem 2 :

3^1/5 ⋅ 3^4/5

Solution :

= 3^1/5 ⋅ 3^4/5

Here two terms are having same base, so we can put only one power and add the exponents.

= 3^{(1/5 + 4/5)}

= 3^(1+4)/5

= 3^5/5

= 3

Problem 3 :

(4^2/3)³

Solution :

= (4^2/3)³

Here we have power raised by another power, so we can multiply the powers.

= 4^{(2/3) ⋅ 3}

= 4²

= 16

Problem 4 :

(10^1/2)⁴

Solution :

= (10^1/2)⁴

Here we have power raised by another power, so we can multiply the powers.

= 10^{(1/2) ⋅ 4}

= 10²

= 100

Problem 5 :

8^5/2/8^1/2

Solution :

= 8^5/2/8^1/2

Both numerator and denominator are having the same base. So, write the base once and subtract the powers.

= 8^{(5/2 - 1/2)}

= 8^(5-1)/2

= 8^4/2

= 8²

= 64

Problem 6 :

7^2/3/7^5/3

Solution :

= 7^2/3 / 7^5/3

Both numerator and denominator are having the same base. So, write the base once and subtract the powers.

= 7^{(2/3 - 5/3)}

= 7^(2-5)/3

= 7^(-3)/3

= 7^-1

= 1/7

Problem 7 :

√3 ⋅ √12

Solution :

= √3 ⋅ √12

Since both are having square roots, so we can put only one square root and multiply the radicands.

= √(3 ⋅ 12)

= √36

Converting square root as exponent, we get

= 36^1/2

= (6²)^1/2

= 6

Problem 7 :

∛5 ⋅ ∛25

Solution :

= ∛5 ⋅ ∛25

Since both are having cube roots, so we can put only one cube root and multiply the radicands.

= ∛(5 ⋅ 25)

= ∛(125)

Decomposing 125, we get

125 = 5³

Writing the cube root in exponential form, we get

= (5³)^1/3

= 5^{3 x 1/3}

= 5

Problem 8 :

∜4 / ∜1024

Solution :

= ∜4 / ∜1024

Since both are having fourth roots, so we can put only one cube root and divide the radicands.

= ∜(4/1024)

= ∜(1/256)

Decomposing 256 and converting the fourth root as 1/4, we get

= (1/4⁴)^1/4

= (1/4)

Problem 9 :

√98/√2

Solution :

= √98 /√2

Since both are having square roots, so we can put only one square root and divide the radicands.

= √(98/2)

= √49

= (7²)^1/2

= 7^{2 x 1/2}

= 7

Problem 10 :

∛(125) / ∛5

Solution :

= ∛(125) / ∛5

Since both are having cube roots, so we can put only one cube root and divide the radicands.

= ∛(125/5)

= ∛25

Writing the cube root in exponential form, we get

= 25^1/3

Decomposing 25, we get

= (5²)^1/3

= 5^{2 x 1/3}

= 5^2/3