SIMPLIFYING EXPRESSIONS WITH NEGATIVE EXPONENTS

To understand negative exponents, first let us see quotient rule.

To get rid of the negative exponent, we have to flip the base.

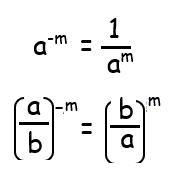
Evaluate the following without using calculator.

Example 1 :

5^-2

Solution :

To change the negative exponent, we will flip the base. Here 5 is the base, it is a integer. We can consider 5 as 5/1.

When we flip 5/1, we get 1/5.

Example 2 :

25^-1/2

Solution :

To change the negative exponent, we will flip the base.

Example 3 :

(16/25)^-3/2

Solution :

Here the base is a fraction, to get rid of the negative exponent, we will flip the base.

The reciprocal of 16/25 is 25/16.

Example 4 :

(4y)^-2

Solution :

Example 5 :

(27b)^1/3 / (9b)^-1/2

Solution :

= (27b)^1/3 / (9b)^-1/2

= (27b)^1/3 ⋅ (9b)^1/2

27 = 3 ⋅ 3 ⋅ 3 ==>  3³  and 9 = 3 ⋅ 3 ==> 3²

= (3³b)^1/3 ⋅ (3²b)^1/2

= 3b^1/3 ⋅ 3b^1/2

=  9 b^{(1/3 + 1/2)}

= 9 b^5/6

Example 6 :

b^-1/2 = 4, what is the value of b ?

Solution :

b^-1/2 = 4

(1/b)^1/2 = 4

To get rid of the exponent 1/2, we take squares on both sides.

((1/b)^1/2)² = 4²

1/b = 16

Take the reciprocal on both sides, we get

b = 1/16

Example 7 :

(2^m)^-6 = 16, what is the value of 2³ x m ?

Solution :

(2^m)^-6 = 16

Here 2^m is the base, when we flip it

2^-6m = 2⁴

Since the bases are equal, we can equate the powers.

-6m = 4

m = -2/3

2³ x m = 8 x (2/3)

= 16/3

Example 8 :

If 4ⁿ = 20, then what is the value of 4^-n ?

Solution :

4ⁿ = 20

Take the reciprocal on both sides

1/4ⁿ = 1/20

4^-n = 1/20

Example 9 :

If a^-1/2 = 3, what is the value of a ?

Solution :

a^-1/2 = 3

Taking squares on both sides, we get

(a^-1/2)² = 3²

a-1  =  9

1/a = 9

a = 1/9

Example 10 :

If 3^x = 10, what is the value of 3^x-3 ?

Solution :

Given :

3^x = 10

3^x-3  = 3^x ⋅ 3^-3

= 10 ⋅ 3^-3

= 10/3³

= 10/27

Example 11 :

A drop of water leaks from a faucet every second. How many liters of water leak from the faucet in 1 hour?

Solution :

1 hour = 60 minutes

1 minute = 60 seconds

1 hour = 60 x 60 ==> 3600 seconds

Water leaks from the faucet at a rate of 50⁻² liter per second. Multiply the time by the rate.

= 3600 x 50⁻²

= 3600 x (1/50²)

= 3600/2500

= 1.44

So, 1.44 liters of water leak from the faucet in 1 hour.

Example 12 :

a)  If a is a nonzero number, does the value of a⁰ depend on the value of a?

b)  Explain how to evaluate 10⁻³

c)  Without evaluating, order 5⁰, 5⁴, and 5⁻⁵ from least to greatest.

Solution :

a)  No, becaause anything to the power of 0 will given the result 1.

b)  To evaluate the value 10⁻³, we should change the negative exponent as positive.

10⁻³ = 1/10³

= 1/(10 x 10 x 10)

= 1/1000

c)  Without evaluating, order 5⁰, 5⁴, and 5⁻⁵ from least to greatest.

Anything to the power 0 will give the result 1. 

To convert the negative exponent as positive exponent, we have write the reciprocal of the given fraction.

By considering all these points, we know that the least value is 5⁻⁵. By arranging from least to greatest, we get

5⁻⁵, 5⁴, 5⁰

Example 13 :

Which is different? Find “both” answers.

a)  Rewrite 1/(3 ⋅ 3 ⋅ 3)   using a negative exponent.

b)  Write 3 to the negative third power.

c)  Write 1/3 cubed as a power.

d)  Write (−3) ⋅ (−3) ⋅ (−3) as a power.

Solution :

a)  1/(3 ⋅ 3 ⋅ 3) = 1/3³

b) 3 to the negative third power = 3^-3

to convert the negative exponent as positive exponent, we get 1/3³

c)  1/3 cubed as a power = (1/3)³ ==> 1/3³

d) (−3) ⋅ (−3) ⋅ (−3)

Since the same number is repeating three times, we use exponential form to write it,Then we get

= (-3)³ 

From the analysis above, statements (a), (b) and (c) are the same and (d) is different.

Example 14 :

Use the Quotient of Powers Property to copy and complete the table.

a) What patterns do you see?

b)  How would you define 5⁰? Why?

c) How can you rewrite 5⁻¹ as a fraction?

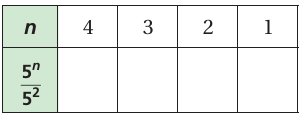
Solution :

5ⁿ/5² = 5^{n - 2}

a) To get the next value, we have to divide the preceeding value by 5.

b)  The value of 5⁰ is 1.

c)  5^-1 = 1/5

Example 15 :

Describe and correct the error in evaluating the expression.

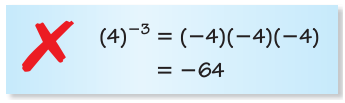
Solution :

Since we have negative exponent, by converting into the reciprocal only we can change the negative exponent to positive exponent.

4^-3 = 1/4³

= 1/(4 x 4 x 4)

= 1/64