SIMPLIFY RADICAL EXPRESSIONS

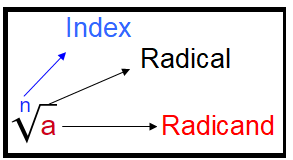
If n is even number, then n^th root of the negative number is not real.

• If we have square root, for every two values or variables inside the square we can take one out of it.
• If we have cube root, for every three values or variables inside the cube root, we can take one out of it.
• If we have fourth root, for every four values or variables inside the fourth root, we can take one out of it.

Simplify the radical expression using the definition.

Example 1 :

√(4(y - 1)²)

Solution :

= 2|y - 1|

Example 2 :

∛(-8x³y⁶)

Solution :

Example 3 :

5^th root (2x - 1)⁵

Solution :

Example 4 :

∜(16x⁸)

Solution :

Example 5 :

∛(-27x³)

Solution :

Example 6 :

∜(16a¹²y²)

Solution :

Example 7 :

√x / ∛x

Solution :

Example 8 :

√(∛x)

Solution :

Example 9 :

√(x + 7)√(x - 7)

Solution :

= √(x + 7)√(x - 7)

= √(x + 7)(x - 7)

Here (x+7)(x-7) looks like (a + b) (a - b) = a² - b²

= √(x + 7)(x - 7)

= √(x² - 7²)

Example 10 :

√50

Solution :

= √50

Decomposing 50 into prime factors, we get

= √(5 ⋅ 5 ⋅ 2)

= 5√2

Example 11 :

Add or subtract the following radicals. Write answers in simplified form. 

Solution :

a)  4√3 - 2√3

Subtracting these two, we get

= 2√3

b) 

= 4√10 + 6√10 - √10 + 2

= 10√10 - √10 + 2

= 9√10 + 2

c)

= 4√x + √x

= 5√x

d) 

= 3√y - 6√y

= - 3√y

e)

= √x + √y + x + 3√y

= √x + x + √y + 3√y

= √x + x + 4√y

f)

= 6√7 - 8√7

= -2√7

g)

= 12√15 + 5√15 - 8√15

= 17√15 - 8√15

= 9√15

h)

= 7√108 - 6√180

Decomposing 108 and 180.

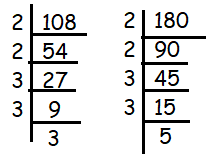
= 7√(2 x 2 x 3 x 3 x 3) - 6√(2 x 2 x 3 x 3 x 5)

= 7 x 2 x 3√3 - 6 x 2 x 3 √5

= 42√3 - 36√5

Example 12 :

Rationalize the denominators and simplify (assume all variables represent positive real numbers).

Solution :

a)  15/√5

Multiplying the numerator and denominator by √5, we get

= (15/√5) ⋅ (√5/√5)

= 15√5/5

= 3√5

b) √32a⁵ b³/√2ab²

= √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ a⁵ ⋅ b³)/√2ab²

= 4a²b√(2ab)/b√2a

= 4a²b√b

c)  2/(3 + √5)

= [2/(3 + √5)] ⋅ [(3 - √5) / (3 + √5)]

= 2⋅ (3 - √5) /(3 + √5) (3 + √5)

= (6 - 2√5) / (3² - √5²)

= (6 - 2√5) / (9 - 5)

= (6 - 2√5) / 4

= (3 - √5) / 2

d)  (2 + √5)/(6 - √3)

= (2 + √5)/(6 - √3) ⋅ [(6 + √3) / (6 + √3)]

= (2 + √5)(6 + √3) / (6 - √3) ⋅(6 + √3)

= (12 + 2√3 + 6√5 + √15) / (6² - √3²)

= (12 + 2√3 + 6√5 + √15) / (36 - 3)

= (12 + 2√3 + 6√5 + √15) / 33

e)  (1 + √2)/(3 + √5)

= (1 + √2)/(3 + √5) ⋅ [(3 - √5) / (3 - √5)]

= (1 + √2)(3 - √5) / (3 + √5)(3 - √5)

= (3 - √5 + 3√2 - √10) / (3² - √5²)

= (3 - √5 + 3√2 - √10) / (9 - 5)

= (3 - √5 + 3√2 - √10) / 4

f)  √18a³√18a³

= √(18a³ ⋅ 18a³)

= 18a³ 

g)  √0.121

= √0.121 ⋅ √(1000/1000)

= √(0.121 ⋅ 1000)/√1000

= √121/√1000

= 11/10√10

= 1.1/√10

h)  (1 + √0.01)/(1 - √0.1)

= (1 + √0.01)/(1 - √0.1) [(1 + √0.1)/(1 + √0.1)]

= (1 + √0.01)(1 + √0.1) / (1 - √0.1)(1 + √0.1)

= (1 + √0.1 + 0.1 + 0.1/√10) / 0.9

= (1.1 + √0.1 + 0.1/√10) / 0.9