SIMPLIFY NEGATIVE EXPONENTS WITH VARIABLES

To simplify the expression involving exponents, we should be aware of rules in exponents.

Product Rule of Exponents :

If we have same bases for two or more terms and they are multiplied, then use only one base and add the powers.

Quotient Rule of Exponents :

If we have same bases for both numerator and denominator , then use only one base and subtract the powers.

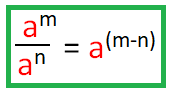
Power of a Power Rule :

When we have power raised to another power, we will multiply the powers.

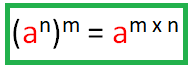
Negative Exponent Rule :

To change the negative exponent as positive, we have two ways.

(i) Change the place

(ii) Take the reciprocal.

Base with negative sign :

If base is having negative sign, we have to consider the power. 

• If the power is odd, the result will also have negative sign.
• If power is even, the result will have positive sign.

Write the expression with only positive exponents. Assume all variables represent non zero numbers. Simplify if necessary.

Problem 1 : 

(3x²)³/x¹⁵

(a) 27/x²¹  (b)  27/x¹⁰  (c)  3/x⁹  (d)  27/x⁹

Solution :

= (3x²)³/x¹⁵

Distributing the power for the terms which are inside the bracket.

= 3³(x²)³/x¹⁵

= 27x⁶/x¹⁵

Using the quotient rule of exponent, combining the powers

= 27 / x^{15 - 6}

= 27 / x⁹

Option d is correct.

Problem 2 : 

(-a)^-18

(a) 1/a¹⁸  (b)  18a  (c)  1/-a¹⁸  (d)  1/a^-18

Solution  :

= (-a)^-18

To convert the negative exponent to positive exponent, we have to write the reciprocal.

= 1/(-a)¹⁸

Now we have negative for the base. By considering the exponent since it is even, the negative base will become positive.

= 1/a¹⁸

So, option a is correct

Problem 3 : 

x^-16/x^-4

(a) 1/x¹²  (b) x¹²  (c)  1/x²⁰  (d)  -x²⁰

Solution  :

= x^-16/x^-4

Using quotient rule of exponent, combining the powers

= x^{-16 + 4}

= x^-12

To change the negative exponent as positive exponent, we get

= 1/x¹²

So, option a is correct.

Problem 4 : 

(-3w³/x)⁴

(a) -81w¹²/x⁴          (b) -81w¹²/x        (c)  81w¹²/x⁴          (d)  81w⁷/x⁴

Solution  :

= (-3w³/x)⁴

Distributing the power for both numerator and denominator.

= (-3w³)⁴/x⁴

Distributing the powers for for the terms which are multiplied inside the bracket in the numerator. We get

= (-3)⁴(w³)⁴/x⁴

Since the power is even and we have negative base, we can change the negative base as positive.

= 81 w¹²/x⁴

So, option c is correct.

Problem 5 : 

m^-9 m⁵ m^-1

(a) 1/m⁵    (b) 1/m⁴   (c)  m⁷   (d)  m⁵

Solution  :

= m^-9m⁵m^-1

= m^(-9+5-1)

= m^{(-10 + 5)}

= m^-5

= 1/m⁵

Problem 6 : 

(2^-2 ⋅ 5^-5)^-4

(a) 2⁸ ⋅ 5²⁰    (b) 1/(2⁷ ⋅ 5⁷)  (c)  1/(2⁸ ⋅ 5²⁰)   (d)  2⁷ ⋅ 5⁷

Solution  :

= (2^-2 ⋅ 5^-5)^-4

Changing the negative exponent as positive, we get

= (1/2² ⋅ 1/5⁵)^-4

= (2² ⋅ 5⁵)⁴

= (2²)⁴ ⋅ (5⁵)⁴

= 2⁸ ⋅ 5²⁰

So, option a is correct.

Problem 7 : 

By what number should (–3)^{– 2} be multiplied so that the product may be equal to 9?

Solution  :

Let x be the numer should be multiplied. The result should be 9.

(–3)^{– 2} ⋅ x = 9

Dividing by (–3)^{– 2} on both sides, we get

x = 9 / (–3)^{– 2}

= 9 x (–3)²

= 9 x 9

= 81

Problem 8 : 

Find the value of x so that

(5/3)^-2 ⋅ (5/3)^-14 = (5/3)^8x

Solution  :

(5/3)^-2 ⋅ (5/3)^-14 = (5/3)^8x

Since we have same bases which are multiplied, using the product rule of exponent/

(5/3)^-2-14 = (5/3)^8x

(5/3)^-16 = (5/3)^8x

On both sides, we have same bases then by equating the powers.

-16 = 8x

x = -16/8

x = -2

Problem 9 : 

If 2^{2x – 3} = (64)^x, find the value of x.

Solution  :

2^{2x – 3} = (64)^x

64 = 2⁶

2^{2x – 3} = (2⁶)^x

2^{2x – 3} = 2^6x

2x - 3 = 6x 

2x - 6x = 3

-4x = 3

x = -3/4

So, the value of x is -3/4.

Problem 10 : 

Find the value of x so that

(-7/11)^-3 ⋅ (-7/11)^5x = [(-7/11)^-2]^-1

Solution  :

(-7/11)^-3 ⋅ (-7/11)^5x = [(-7/11)^-2]^-1

(-7/11)^-3+5x  = (-7/11)²

-3 + 5x = 2

5x = 2 + 3

5x = 5

x = 5/5

x = 1

So, the value of x is 1.

Problem 11 : 

Find the value of x so that

(3/7)^{-2x + 1} / (3/7)^-1 = [(3/7)^-1]^-7

Solution  :

(3/7)^{-2x + 1} / (3/7)^-1 = [(3/7)^-1]^-7

(3/7)^{-2x + 1 + 1} = (3/7)^-1(-7)

(3/7)^{-2x + 2} = (3/7)⁷

-2x + 2 = 7

-2x = 7 - 2

-2x = 5

x = -5/2

So, the value of x is -5/2.

Problem 12 : 

If p/q = (5/2)^-2 x (4/3)⁰ , find the value of (p/q)^-2

Solution  :

p/q = (5/2)^-2 x (4/3)⁰

= (2/5)² x 1

= (4/25)

The value of p/q is 4/25

Finding the value of  (p/q)^-2 :

(p/q)^-2 = (4/25)^-2

To convert the negative exponent as psotive exponent, we get

= (25/4)²

= 625/16

So, the value of  (p/q)^-2 is 625/16.