SET UP THE DEFINTE INTEGRAL THAT GIVES THE AREA OF THE SHADED REGION

Set up a definite integral that yields the area of the region and evaluate.

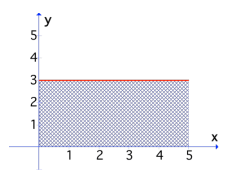
Problem 1 :

f(x) = 3

Solution :

Set up the definite integral :

a = 0, b = 5, equation of the curve : f(x) = 3

Evaluating the definite integral :

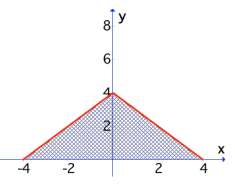
Problem 2 :

f(x) = 4 - |x|

Solution :

Decomposing the given function into two parts.

f(x) = 4 - x

By observing the given figure, y-axis is dividing the required area into two equal parts.

Set up the definite integral :

a = 0, b = 4, required function : f(x) = 4 - x

Evaluating the definite integral :

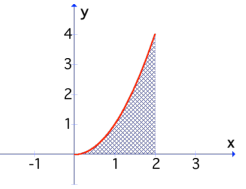
Problem 3 :

f(x) = x²

Solution :

a = 0, b = 2, equation of the curve : f(x) = x²

Set up the definite integral :

Evaluating the definite integral :

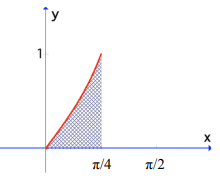
Problem 4 :

f(x) = tan x

Solution :

a = 0, b = π/4, equation of the curve : f(x) = tan x

Set up the definite integral :

Evaluating the definite integral :

Problem 5 :

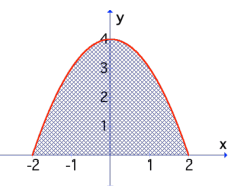
f(x) = 4 - x²

Solution :

f(x) = 4 - x²

By observing the given figure, y-axis is dividing the required area into two equal parts.

Set up the definite integral :

a = 0, b = 2, required function : f(x) = 4 - x²

Evaluating the definite integral :

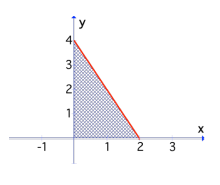
Problem 6 :

f(x) = 4 - 2x

Solution :

Set up the definite integral :

Evaluating the definite integral :