ROW REDUCTION FOR A SYSTEMS OF LINEAR EQUATIONS

The process of solving system using elementary row operations is known as row reduction. Our aim is to perform row operations until there are all zeroes in the bottom left hand corner. At this time the system is said to be in echelon form.

Elementary row operations equivalent to the three legitimate operations with equations. 

• Interchanging rows
• Replace any row by a non zero multiple of itself
• Replace any row by itself plus or minus a multiple of another row.

Unique solution
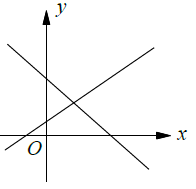No solution
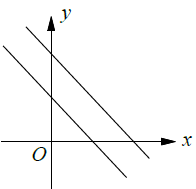Infinitely many solution

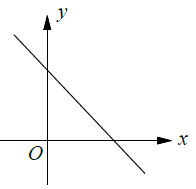Use row operations to solve the following systems of linear equations.

Problem 1 :

2x + 3y = 4

5x + 4y = 17

Solution :

In augmented matrix form the system is :

R₂ --> 2R₂ - 5R₁

10     8      34

10     15      20

(-)    (-)      (-) 

______________

0       -7      14

After using row reduction operation, we get the above matrix. From second row, we get

-7y = 14

Dividing by -7, we get

y = -2

From the first row,

2 x + 3y = 4

2x + 3(-2) = 4

2x - 6 = 4

2x = 4 + 6

2x = 10

x = 5

So, the required solution is (5, -2).

Problem 2 :

x - 2y = 8

4x + y = 5

Solution :

In augmented matrix form the system is :

R₂ --> 4R₁ - R₂

 4      -8      32

4       1       5

(-)       (-)    (-)

---------------------------

0       -9      27

After using row reduction operation, we get the above matrix. From second row, we get

-9y = 27

Dividing by -9, we get

y = -3

From the first row,

x - 2y = 8

x - 2(-3) = 8

x + 6 = 8 

x = 8 - 6

x = 2

So, the required solution is (2, 3).

Problem 3 :

4x + 5y = 21

5x - 3y = -20

Solution :

In augmented matrix form the system is :

R₂ --> 5R₁ - 4R₂

20      25      105

20     -12       -80

(-)     (+)      (+)

---------------------------

0       37      185

After using row reduction operation, we get the above matrix. From second row, we get

37y = 185

Dividing by 37, we get

y = 5

From the first row,

4x + 5y = 21

4x + 5(5) = 21

4x + 25 = 21

4x = 21 - 25

4x = -4

x = -1

So, the required solution is (-1, 5).

Problem 4 :

3x + y = -10

2x + 5y = -24

Solution :

In augmented matrix form the system is :

R₂ --> 2R₁ - 3R₂

6        2      -20

  6      15      -72

(-)     (-)      (+)

---------------------------

0       -13      52

After using row reduction operation, we get the above matrix. From second row, we get

-13y = 52

Dividing by -13, we get

y = -4

From the first row,

3x + y = -10

3x + (-4) = -10

3x - 4 = -10

3x = -10 + 4

3x = -6

x = -6/3

x = -2

So, the required solution is (-2, -4)

Problem 5 :

Use row reduction on the system 

2x + 3y = 5

2x + 3y = 11

to reduce the system to 

b) What does the second row indicate ?

c) Explain this result geometrically 

Solution :

Since no more variable terms is no more variable terms and there is constant in echelon form, there is no solution.

b) The second row indicate that there is no solution for the system of linear equations given.

c)  Since there is no solution, the lines will never meet each other and they are parallel.

Problem 6 :

a) Use row reduction to the system

2x + 3y = 5

4x + 6y = 10

to reduce the system to 

b) Explain this result geometrically.

Solution :

a) By considering the second row, including variable and constants everything is 0. Then there is infinitely many solution.

b) The lines are coincident lines.

Problem 7 :

Consider the equation pair

x + 2y = 3

2x + 4y = 6

a) Explain why there are infinitely many solutions, giving geometric evidence.

b)  Explain why the second equation can be ignored when finding all solutions.

c)  Give all solutions in form,

i)  x = ?, y = ?

ii) y = s, x = ?

Solution :

In augmented matrix form the system is :

R₂ --> 2R₁ - R₂

2        4       6

  2        4       6

(-)     (-)      (-)

---------------------------

0         0       0

a) The second equation is the same as the first when divided throughout by 2. The lines are coincident.

b) It gives no more information than the first..

c)  Give all solutions in form,

i)  When x = t

x + 2y = 3

Applying x = t, we get

t + 2y = 3

2y = 3 - t

y = (3 - t)/2

ii) When y = s

x + 2y = 3

Applying y = s, we get

x + 2s = 3

x = 3 - 2s