REVIEW PROBLEMS ON QUADRATIC FUNCTIONS AND EQUATIONS

Problem 1 :

Write an equation for the parabola whose vertex is at (3, 6) and which passes through (4, 4).

a. y = -2(x + 3)² – 6                    c. y = 2(x - 3)² + 6

b. y = (x + 3)² – 6                        d. y = -2(x - 3)² + 6 

Solution :

Vertex = (3, 6)

Passes through the point = (4, 4)

y = a(x – h)² + k

x = 4, y = 4

h = 3, k = 6

By applying the vertex, we get

y = a(x – 3)² + 6 --- (1)

By applying the point passes through the parabola, we get

4 = a(4 – 3)² + 6

4 = a + 6

4 – 6 = a

-2 = a

a = -2 in equation (1)

y = -2(x – 3)² + 6

So, option (d) is correct.

Problem 2 :

Solve the quadratic equation :

x² + 10x + 22 = 0

a. 5 ± 2√7        c.100 ± √3

b. -5 ± √3        d.-10 ± 2√7

Solution :

x² + 10x + 22 = 0

This quadratic equation is not factorable, using formula we can solve it.

a = 1, b = 10, c = 22

x = -b ± √(b² – 4ac)/2a

= (-10 ± √((10)² – 4(1)(22)))/2(1)

= (-10 ± √(100 – 88))/2

= -10/2 ± √12/2

= -5 ± √(4 × 3)/2

= -5 ± 2√3/2

= -5 ± √3

So, option (b) is correct.

Problem 3 :

The function y = -16t² + 248 models the height y in feet of a stone t seconds after it is dropped from the edge of a vertical cliff. How long will it take the stone to hit the ground ? Round to the nearest hundredth of a second.

a. 7.87 seconds       c. 3.94 seconds

b. 0.25 seconds        d. 5.57 seconds

Solution :

Given, y = -16t² + 248

When y = 0

0 = -16t² + 248

248 = 16t²

248/16 = t²

√248/16 = t

√31/2 = t

√15.5 = t

3.94 = t

So, 3.94 seconds long will it take the stone to hit the ground.

So, option (c) is correct.

Problem 4 :

Use a graphing calculator to solve the equation -10x² – 2x + 3 = 0. If necessary, round to the nearest hundredth.

a. – 0.46, 0.66       c. -0.66, 0.46

b. -1.31, 0.91         d. -0.56, 0.56

Solution :

Given, -10x² – 2x + 3 = 0

x = -b ± √(b² – 4ac)/2a

a = -10, b = -2, c = 3

= (2 ± √(2² – 4(-10)(3)))/2(-10)

= (2 ± √(4 + 120))/(-20)

= (2 ± √124)/(-20)

= (2 ± √(31 × 4))/(-20)

= (2 ± 2√31)/(-20)

= 2/(-20) ± 2√31/(-20)

= (-1 ± √31)/10

x = (-1 + √31)/10, (-1 - √31)/10    

= (-1 + 5.568)/10, (-1 – 5.568)/10

= 4.568/10, -6.568/10

= 0.46, -0.66

So, option (c) is correct.

Problem 5 :

Solve the equation.

36x² + 4 = 0

a. -1/3i, 1/3i           c. -1/9i, 1/9i

b.  -1/3, 1/3           d. -3i, 3i

Solution :

36x² + 4 = 0

36x² = -4

x² = -4/36

x² = -1/9

x = ±√-1/9

x = ±√(-1 × 1/9)

x = ±i√1/9

x = 1/3i, -1/3i  

So, option (a) is correct.

Problem 6 :

Which is the graph of y = (x – 2)² + 4?

a)

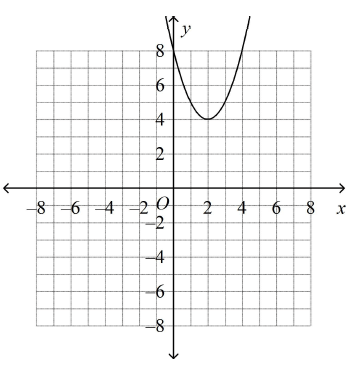
b)

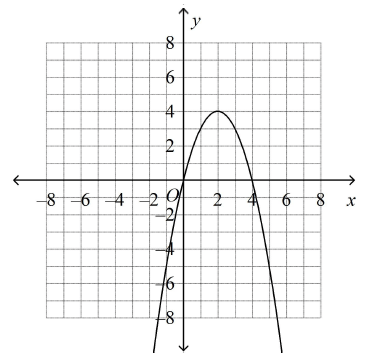
c)

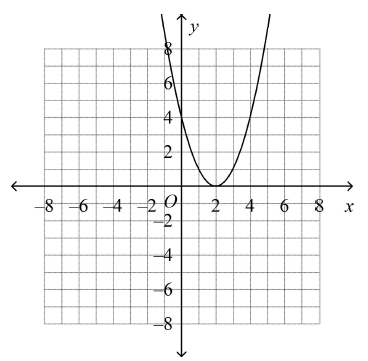
d)

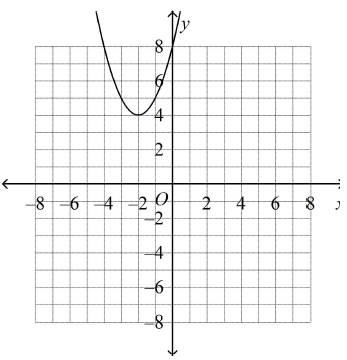
Solution :

y = (x – 2)² + 4

Comparing the equation given above with y = a(x - h)² + k

a = 1 > 0. Then parabola opens up. Vertex is at  (2, 4).

To find x-intercept, put y = 0

(x – 2)² + 4 = 0

(x – 2)² = -4

There is no x-intercept. So, option a is correct.

Problem 7 :

Solve by factoring.

4x² + 10x – 24 = 0

a.  3/2, -1        c. 4, -1

b. -4, 3/2        d. -4, 4

Solution :

4x² + 10x – 24 = 0

2(2x² + 5x – 12) = 0

Dividing 2 on both sides.

2x² + 5x – 12 = 0

By using algebraic expression

2x² + 8x – 3x – 12 = 0

2x(x + 4) – 3(x + 4) = 0

(2x – 3) (x + 4) = 0

2x – 3 = 0 and x + 4 = 0

2x = 3

x = 3/2 , x = -4

So, option (b) is correct.

Problem 8 :

Identify the vertex and the y – intercept of the graph of the function y = 2(x + 2)² – 2.

a. vertex : (2, 2), y – intercept : 8 

b. vertex : (-2, -2), y – intercept : 6

c. vertex : (2, -2), y – intercept : 6

d. vertex : (-2, 2), y – intercept : 2

Solution :

y = 2(x + 2)² – 2

Comparing the given equation with,

y = a(x - h)² + k

Vertex is at (h, k) ==> (-2, -2). 

To find y-intercept, put x = 0

y = 2(0 + 2)² – 2

y = 2(4) – 2

y = 6

y – intercept = 6

So, option (b) is correct.

Problem 9 :

y = 3x² – 36x + 111. What is the minimum value of the function ?

Solution :

To get maximum or minimum value of the quadratic function, we have to write it in the vertex form.

y = 3(x² – 12x) + 111

y = 3(x² – 2 ⋅ 6 ⋅ x + 6² - 6²) + 111

y = 3[(x – 6)² - 6²] + 111

y = 3[(x – 6)² - 36] + 111

y = 3(x – 6)² - 108 + 111

y = 3(x – 6)² + 3

a = 3 > 0, the parabola opens up. So, it will have minimum value.

Vertex is at (6, 3)

So, the minimum value is at y = 3.

Problem 10 :

Use vertex form to write the equation of the parabola. 

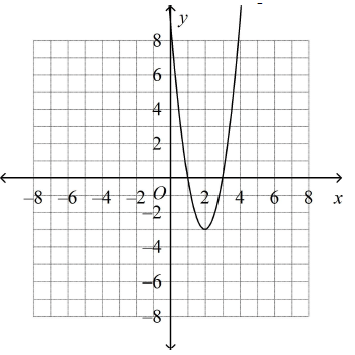
a. y = (x – 2)² – 3        c.  y = 3(x - 2)² - 3

b. y = 3(x + 2)² – 3       d. y = 3(x + 2)² + 3

Solution :

The equation of the parabola y = a(x – h)² + k

Vertex = (2, -3)

= a(x – 2)² – 3

Passes through the point (1, 0)

a – 3 = 0

a = 3

a = 3 substitute in equation a(x – 2)² – 3.

= 3(x – 2)² – 3