QUESTIONS ON PRIME FACTORIZATION

Write the prime factorization of the number:

Problem 1 :

20

Solution :

Decompose 20 into prime factors,

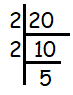
20 = 2 x 2 x 5

Writing the repeating factors in exponential form, we get

= 2² x 5

Problem 2 :

72

Solution :

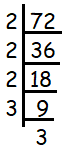
72 = 2 x 2 x 2 x 3 x 3

Here 2 is repeating two times and 3 is repeating three times. Writing the repeating factors in exponential form, we get

72 = 2³ x 3²

Problem 3 :

68

Solution :

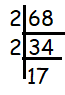
68 = 2 x 2 x 17

Here 2 is repeating two times. Writing the repeating factors in exponential form, we get

68 = 2² x 17

Problem 4 :

55

Solution :

55 = 5 x 11

Here no factor is repeating, so no need to use exponential form.

Problem 5 :

30

Solution :

30 = 2 x 5 x 3

Here there is no repeating factor, so no need to use the exponential form.

Problem 6 :

74

Solution :

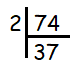
Here 37 is prime number, so we stop the process here itself.

74 = 2 x 37

Problem 7 :

105

Solution :

105 = 5 x 3 x 7

There is no repeating factor.

Problem 8 :

108

Solution :

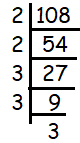
108 = 2 x 2 x 3 x 3 x 3

Here 2 is repeating two times and 3 is repeating three times.

108 = 2² x 3³

Problem 9 :

90

Solution :

90 = 2 x 5 x 3 x 3

= 2 x 5 x 3²

Problem 10 :

198

Solution :

198 = 2 x 3 x 3 x 11

Here 3 is repeating two times. So,

= 2 x 3² x 11

Problem 11 :

Which number is a prime factor of 572?

a) 4     b) 7      c) 13      d)  22

Solution :

572 = 2 x 2 x 11 x 13

Writitng in exponential form, we get

= 2² x 11 x 13

2, 11 and 13 are prime factors. Accordingly options given, option c is correct.

Problem 12 :

What is the prime factorization of 1100?

Solution :

1100 = 11 x 100

= 11 x 2 x 2 x 5 x 5

= 11 x 2² x 5²

So, the prime factorization of 1100 is 11 x 2² x 5².

Problem 13 :

Which of the following is pair of co-primes? 

a)  (16, 62)     b) (18, 25)    c)  (21, 35)     d)  (23, 92)

Solution :

Option a :

  (16, 62)

16 is composite number

62 is also composite number

16 = 2⁴

62 = 2 x 31

Highest common factor of 16 and 62 is 2. Since the highest common factor is not 1, these are not co-primes.

Option b :

  (18, 25)

18 is composite number

25 is also composite number

18 = 2 x 3 x 3

= 2 x 3²

25 = 5 x 5

= 5²

Highest common factor of 18 and 25 is 1. So, these are co-primes.

Problem 14 :

The greatest number of four digits which is divisible by 15, 25, 40 and 75.

a)  9000     b) 9400    c)  9600     d)  9800

Solution :

15 = 3 x 5

25 = 5 x 5 ==> 5²

40 = 2 x 2 x 2 x 5

= 2³ x 5

75 = 5 x 5 x 3

= 5² x 3

To find the number which is divisible by the numbers 15, 25, 40 and 75 must be a highest common factor.

highest common factor = 3 x 5² x 2³

= 600

Multiples of 600 are also divisble by the given numbers.

600, 1200, 1800, 2400, ............9600

So, option c is correct.

Problem 15 :

The least number should be added to 2497 so that the sum is exactly divisible by 5, 6, 4 and 3 is 

a)  3         b) 13       c)  23       d)  33

Solution :

If the number should be divisible by 5, 6, 4 and 3, then it must be multiple of all these numbers. By finding the least number which is multiple of 5, 6, 4 and 3.

6 = 2 x 3

4 = 2²

least common multiple = 2² x 3 x 5

= 60

Multiples of 60 are also divisible by 5, 6, 4 and 3.

60, 120, 180, ...........

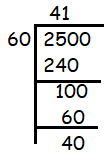
2500 - 40 = 2460

2460, 2520, ..............

2497 - 2520 ==> 23

So, option c is the number should be added to 2497.