PROPORTIONAL RELATIONSHIP

Problem 1 :

Determine if each of the following equations represents a proportional or nonproportional relationship.

(i)  d = 65t

(ii)  p = 0.1s + 2000

(iii)  n = 450 − 3p

(iv)  36 = 12d

A linear relationship is a proportional relationship when y/x is constant. Otherwise, the linear relationship is nonproportional.

Solution :

(i)  d = 65t

Since the given equation is in the form of y = kx, it is a proportional relationship.

Constant of proportionality = 65.

(ii)  p = 0.1s + 2000

0.1s is added by 2000. So, it is not in proportional relationship.

(iii)  n = 450 − 3p

By rewriting as, n = -3p + 450

-3p is added by 450. It is not a proportional relationship.

(iv)  36 = 12d

There is no relationship between two variables. So, there is no proportional relationship.

From the Table

Problem 2 :

Determine if the linear relationship represented by each table is a proportional or nonproportional relationship.

(i) When x = 2, y = 30

When x = 8, y = 90

Solution :

When x = 2, y = 30

Constant of proportionality (k) = y/x

k = 30/2 ==>  15

When x = 8, y = 90

k = 90/8 ==>  45/4

Since constant of proportionality are not equal, it is not in proportional relationship.

(ii)

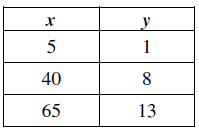
Solution :

When x = 5, y = 1

Constant of proportionality (k) = y/x

k = 1/5

When x = 40, y = 8

k = 8/40 ==>  1/5

Since constant of proportionality are equal, it is in proportional relationship.

From the Statement

Problem 3 :

Determine which situation is a proportional relationship and which situation is a nonproportional relationship.

(i)  The cost for Test Prep Center A is $20 times the number of hours that you attend. 

Solution :

Let C be the cost for test preparation center A.

h be the number of hours.

C = 20h

It is a proportional relationship.

(ii)  The cost for Test Prep Center B is $25 an hour, but you have a $100 coupon that you can use to reduce the cost.

Solution :

C = 100 - 25h

It is non proportional relationship.

From the Graph

Problem 4 :

Determine if each relationship is a proportional or nonproportional situation.

(i)

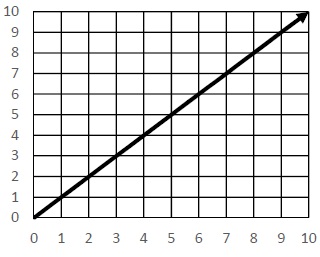
Solution :

Since the line passes through the origin, it is a proportional relationship.

(ii)

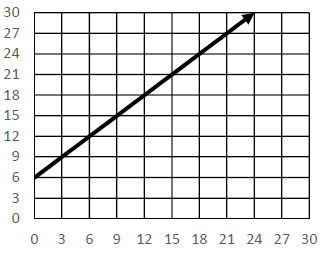
Solution :

Since the line does not passes through the origin, it is a non proportional relationship.

Problem 5 :

You swam for 16 minutes and completed 20 laps. You swam your first 4 laps in 2.4 minutes. How long does it take you to swim 10 laps?

Solution :

Compare unit rates to determine whether the number of laps is proportional to your time. If it is, then you can use ratio reasoning to find the time it takes you to swim 10 laps.

Time taken to complete 20 laps = 16 minutes

Time taken to complete 1 lap = 16/20

= 4/5

= 0.8 lap per minute

Time taken to cover 4 laps = 2.4 minutes

Time taken to complete 1 lap = 2.4/4

= 0.6 laps per minute

The number of laps is not proportional to the time. So, you cannot use ratio reasoning to determine the time it takes you to swim 10 laps.

Problem 6 :

Find the heart rates of yourself and your friend. Do these rates form a proportion? Explain.

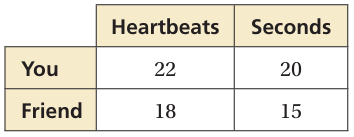
Solution :

Ratio between heartbeat to seconds

The rates are not equal, then they are not in proportion.

Problem 7 :

You earn $56 walking your neighbor’s dog for 8 hours. Your friend earns $36 painting your neighbor’s fence for 4 hours. Are the pay rates equivalent? Explain.

Solution :

Ratio between walking your neighbor's dog to number of hours working :

= 56 : 8

= 7 : 1

Ratio between painting your neighbor's fence to number of hours working :

= 36 : 4

= 9 : 1

The ratios are not equal, then they are not in proportion.

Problem 8 :

The shadow of the moon during a solar eclipse traveled 2300 miles in 1 hour. In the first 20 minutes, the shadow traveled 766  2/3 miles. How long did it take for the shadow to travel 1150 miles? Justify your answer.

Solution :

Distance traveled = 766  2/3 miles 

Time taken = 20 minutes

Converting minutes into hours, we get

= 20/60

= 1/3 hours

766  2/3 miles covered in 1/3 hours, then how long it will take to cover 1150 miles.

766  2/3 : 1/3 = 1150 : x

766  2/3 / (1/3) = 1150/x

(2300/3) (3/1) = 1150/x

2300 = 1150/x

x = 1150/2300

x = 1/2 hour

To travel 1150 miles, will be taking 1/2 hour.