PROBLEMS ON THE SUM OF ANGLES AROUND A POINT

The sum of the sizes of the angles at a point is 360°.

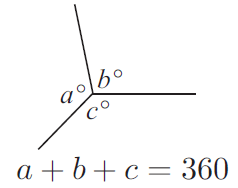
Find the unknown of the following :

Problem 1 :

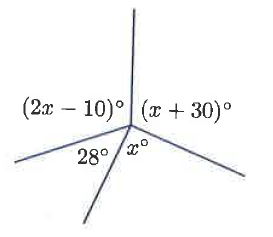
Solution :

2x - 10 + 28 + x + x + 30 = 360

4x - 10 + 28 + 30 = 360

4x + 48 = 360

Subtracting 48 on both sides.

4x = 360 - 48

4x = 312

Dividing by 4 on both sides.

x = 312 / 4

x = 78

Problem 2 :

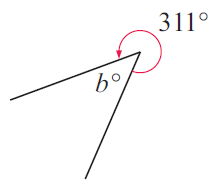
Solution :

b + 311 = 360

Subtracting 311 on both sides.

b = 360 - 311

b = 49

Problem 3 :

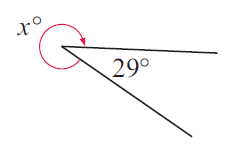
Solution :

29 + x = 360

Subtracting 29 on both sides.

x = 360 - 29

x = 331

Problem 4 :

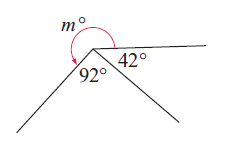
Solution :

m + 92 + 42 = 360

m + 134 = 360

Subtracting 134 on both sides.

m = 360 - 134

m = 226

Problem 5 :

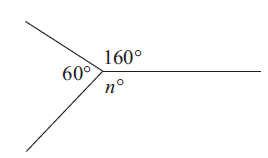
Solution :

60 + 160 + n = 360

220 + n = 360

Subtracting 220 on both sides.

n = 360 - 220

n = 140

Problem 6 :

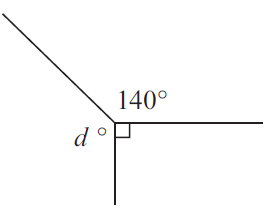
Solution :

d + 90 + 140 = 360

d + 230 = 360

Subtracting 230 on both sides.

d = 360 - 230

d = 130

Problem 7 :

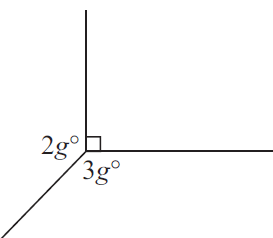
Solution :

2g + 3g + 90 = 360

5g + 90 = 360

Subtracting 90 on both sides.

5g = 360 - 90

5g = 250

Dividing by 5 on both sides.

g = 250/5

g = 50

Problem 8 :

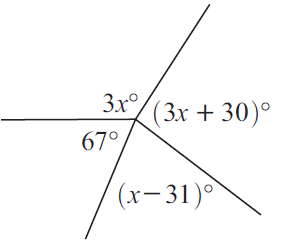
Solution :

3x + 3x + 30 + x - 31 + 67 = 360

7x + 30 + 67 - 31 = 360

7x + 97 - 31 = 360

7x + 66 = 360

Subtracting 66 on both sides.

7x = 360 - 66

7x = 294

Dividing by 7 on both sides.

x = 294/7

x = 42

Problem 9 :

Tell whether the statement is always, sometimes, or never true. Explain your reasoning.

a) Complementary angles are adjacent.

b) Angles in a linear pair are supplements of each other.

c) Vertical angles are adjacent.

d)  Vertical angles are supplements of each other.

e) If an angle is acute, then its complement is greater than its supplement.

f)  If two complementary angles are congruent, then the measure of each angle is 45°.

g) Explain why the supplement of an acute angle must be obtuse.

h) Explain why an obtuse angle does not have a complement.

Solution :

a) Complementary angles are adjacent.

If the sum of two angles is 90 degree, then we say the angles are complementary. It is not necessary to be next to each other or adjacent. Then it is some times.

b) Angles in a linear pair are supplements of each other.

True, linear pair means they must be supplementary by adding those two angle measures we must get 180 degree. So, it is always true.

c) Vertical angles are adjacent.

Vertical angles lie or face each other opposite. So, they are not adjacent angles. Then it is never true.

d)  Vertical angles are supplements of each other.

When two lines are intersecting each other 90 degree, then the sum of vertical angles must be 180. So, it is sometime true.

e) If an angle is acute, then its complement is greater than its supplement.

Let x be the acute angle, then its complementary angle will be 90 - x and its supplementary angle will be 180 - x.

Let us assume x = 30

90 - 30 ==> 60

180 - 30 ==> 150

So, the given statement is never true.

f)  If two complementary angles are congruent, then the measure of each angle is 45°.

Yes, it is always true. 

Let x be the angle, then its complement will be 90 - x

x = 90 - x

x + x = 90

2x = 90

x = 90/2

x = 45

So, it is always true.

g) Explain why the supplement of an acute angle must be obtuse.

Let x be the acute angle (which is lesser than 90 degree).

Its supplement will be 180 - x and it must be greater than 90 degree. Then the given statement is always true.

h) Explain why an obtuse angle does not have a complement.

The measure of obtuse angle must be greater than 90, it will not have complement. Because the angle and its complement should add upto 90 degree. Then it is never true.

Problem 10 :

When viewed from the side, the frame of a ball-return net forms a pair of supplementary angles with the ground. Find m∠BCE and m∠ECD

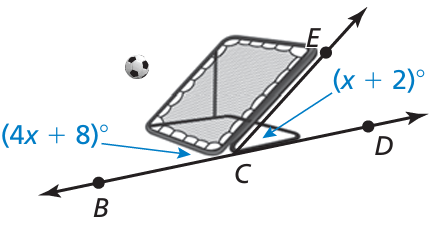
Solution :

m∠BCE + m∠ECD = 180

4x + 8 + x + 2 = 180

5x + 10 = 180

5x = 180 - 10

5x = 170

x = 170/5

x = 34

Applying the value of x in m∠BCE = 4x + 8

= 4(34) + 8

= 136 + 8

= 144

Applying the value of x in m∠ECD = x + 2

= 34 + 2

= 36

So, the required angles are 144 and 36 degree respectively.