PROBLEMS ON SOLVING COMPOUND INEQUALITIES

There are two operators in inequality. Those are 

i)  And

ii)  or

How we use the operator and ?

The region that satisfies both conditions can be fixed as solution. n - and

How we use the operator Or ?

The region that satisfies any one of the conditions can be fixed as solution. u - or

Problem 1 :

(-∞, 1/2) ∩ [-3, 4)

To find the intersection, graph each interval separately. Then find the real numbers common to both intervals.

Problem 2 :

(-∞, -2) ∪ [-4, 3)

Solve the compound inequalities. Write the answers in interval notation.

Problem 1 :

-2 ≤ 3x – 1 ≤ 5

Solution : 

-2 ≤ 3x – 1 ≤ 5

Add 1 on both sides.

-2 + 1 ≤ 3x – 1 + 1 ≤ 5 + 1

-1 ≤ 3x ≤ 6

Divide by 3 on both sides.

-1/3 ≤ x ≤ 2

Problem 2 :

(-3/5)x – 1 ≤ 8 or (-2/3)x ≥ 16

Solution : 

Solving (-3/5)x – 1 ≤ 8 :

Taking the least common multiple, we get

-3x – 5 ≤ 40

Add 5 on both sides.

-3x – 5 + 5 ≤ 40 + 5

-3x ≤ 45

Divide by -3 on both sides.

x ≥ -15

Solving (-2/3)x ≥ 16 :

(-2/3)x ≥ 16

Multiplying by 3 on both sides

-2x ≥ 48

Dividing by -2

x ≤ -24

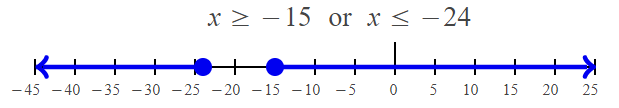
Problem 3 :

-2x – 3 > -3 and x + 3 ≥ 0

Solution : 

Solving -2x – 3 > -3 :

-2x – 3 > -3

Add 3 on both sides.

-2x – 3 + 3 > -3 + 3

-2x > 0

x < 0

Solving x + 3 ≥ 0 :

Subtracting 3 on both sides

x + 3 - 3 ≥ 0 - 3

x ≥ -3

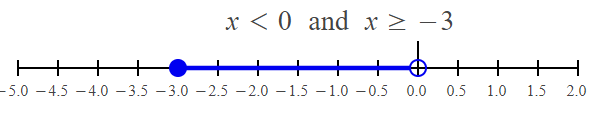
Problem 4 :

5x + 1 ≤ 6 or 2x + 4 > -6

Solution : 

Solving 5x + 1 ≤ 6 :

5x + 1 ≤ 6

Subtract by 1 on both sides.

5x + 1 - 1 ≤ 6 – 1

5x ≤ 5

Divide by 5 on both sides.

5/5x ≤ 5/5

x ≤ 1

Solving 2x + 4 > -6 :

2x + 4 > -6

Subtract by 4 on both sides.

2x + 4 - 4 > -6 – 4

2x > -10

Divide by 2 on both sides.

2/2x > -10/2

x > -5

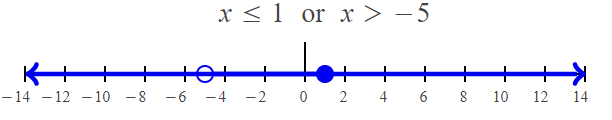
Problem 5 :

2x – 3 > 1 and x + 4 < -1

Solution : 

Solving 2x – 3 > 1 :

Add 3 on both sides.

2x > 1 + 3

2x > 4

Divide by 2 on both sides.

2/2x > 4/2

x > 2

Solving x + 4 < -1 :

Subtract by 4 on both sides.

x < -1 – 4

x < -5

The solution region should satisfy both x > 2 and x < -5. So, there is no solution.