PROBLEMS ON SIMILAR TRIANGLES FOR SAT PRACTICE

Problem 1 :

A summer camp counselor wants to find a length, x, in feet, across a lake as represented in the sketch above. The lengths represented by AB, EB, BD, and CD on the sketch were determined to be 1800 feet, 1400 feet, 700 feet, and 800 feet, respectively.  Segments AC and DE intersect at B and  ∠AEB  and ∠CDB have the same measure. What is the value of x?

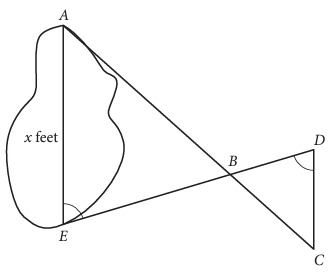
Solution :

Considering triangles ABE and BDC

∠AEB = ∠BDC (Given)

∠ABE = ∠DBC (Vertically opposite angles)

Using AA triangles ABE and BDC are similar.

AB = 1800 ft, EB = 1400 ft, BD = 700 ft and CD = 800 ft

x = 1600 ft

Problem 2 :

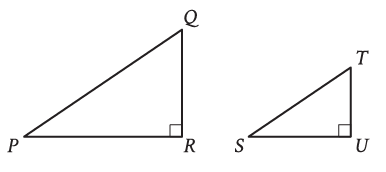
Right triangles PQR and STU are similar, where P corresponds to S. If the measure of angle Q is 18°, what is the measure of angle S?

A) 18°      B) 72°      C) 82°    D) 162°

Solution :

Since the two right triangles PQR and STU are similar, corresponding angles will be equal.

∠P = ∠S

∠Q = ∠T

∠R = ∠U

Sum of interior angles of triangle = 180

∠P + ∠Q + ∠R = 180 and ∠S + ∠U + ∠T = 180

∠P + 18 + 90 = 180

∠P  = 180 - 108

∠P  = 72

Then, ∠S  = 72

Problem 3 :

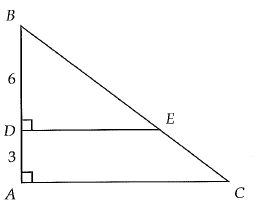
In the figure above, AD = 3, BD = 6 and BC = 15. What is the area of trapezoid ADEC ?

Solution :

Considering triangles BDE and BAC.

∠BDE = ∠BAC

∠DBE = ∠ABC

In triangle ABC,

BC² = BA² + AC²

15² = 9² + AC²

AC² = 225 - 81

AC² = 144

AC = 12

Let BE = x, EC = 15 - x

In triangle ABC,

BE² = BD² + DE²

10² = 6² + DE²

DE² = 100 - 36

DE² = 64

DE = 8

Area of trapezium = (1/2) x h x (sum of parallel sides)

= (1/2) x 3 x (8 + 12)

= (1/2) x 3 x 20

= 30 square units.

Problem 4 :

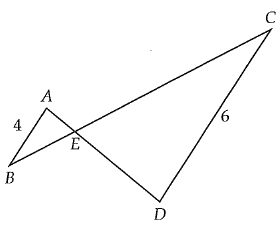
In the figure above, AB is parallel to CD. If BC = 15, what is the length of EC ?

Solution :

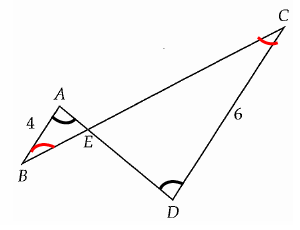
Alternative interior angles are equal. So, triangles ABE and EDC are similar. Then ratio between corresponding sides will be ratio.

AB/CD = BE/EC = AE/ED

Let BE = x, then EC = 15 - x

4/6 = x/(15 - x) = AE/ED

4(15 - x) = 6x

60 - 4x = 6x

60 = 10x

x = 6

EC = 15 - 6

EC = 9

Problem 5 :

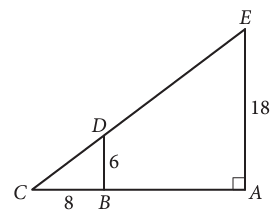
In the figure above, BD is parallel to AE. What is the length of CE ?

Solution :

Considering triangles CBD and CAE,

∠DCB = ∠ECA (common)

∠DBC = ∠EAC (right angle)

So, triangles CBD and CAE are similar.

Comparing the corresponding sides,

CD/CE = DB/AE = CB/CA

Applying the known values for DB/AE = CB/CA

Let BA = x

6/18 = 8/(8+x)

1/3 = 8/(8+x)

8 + x = 8(3)

8 + x = 24

x = 24 - 8

x = 24 - 8

x = 16 (Measure of BA)

Considering the large triangle CAE, using Pythagorean theorem

CE² = CA² + AE²

CE² = (CB + AB)² + AE²

CE² = (8+16)² + 18²

CE² = 24² + 18²

CE² = 576 + 324

CE² = 900

CE = 30

So, the length of CE is 30.

Problem 6 :

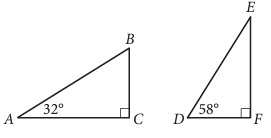
Triangles ABC and DEF are shown above. Which of the following equal to the ratio BC/AB ?

a)  DE/DF     b)  DF/DE      c)  DF/EF        d)  EF/DE

Solution :

∠BCA = ∠EFD (right angles)

In triangle ABC,

sum of interior angles of triangle = 180

∠A + ∠B + ∠C = 180

32 + ∠B + 90 = 180

∠B = 180 - 122

∠B = 58

So, corresponding angles are 

∠B and ∠D, ∠A and ∠E, ∠C and ∠F

Comparing corresponding sides, we get

BC/DF = AC/EF = AB/DE

BC/DF = AB/DE

BC/AB = DF/DE

So, option b is correct.

Problem 7 :

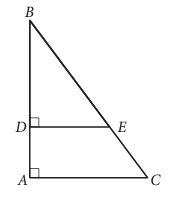
In the figure above, tan B = 3/4. If BC = 15 and DA = 4, what is the length of DE ?

Solution :

Considering triangles BDE and ABC,

∠BDE = ∠BAC

∠DBE = ∠ABC

The triangles are similar.

Both triangles BDE and ABC are 3-4-5 right triangles. In triangle BDE, the measure of BE is 5 and BC = 15, which means triangles BDE and ABC are in the ratio 1 : 3.

DB and AB are in the ratio 1 : 3

AC = 3 x 3 ==> 9

AB = 4 x 3 ==> 12

DB = 12 - 4 ==>8

DA = 4, DB = 8

which means that the similarity ratio of ΔDBE to the 3-4-5 triangle is 2:1 (DB is the side adjacent to angle B). Therefore, the length of DE , which is the side opposite to angle B, is

3 × 2 = 6.