PROBLEMS ON SCATTER PLOT AND LINE OF BEST FIT

Problem 1 :

The table shows the weekly sales of a DVD and the number of weeks since its release. Write an equation that models the DVD sales as a function of the number of weeks since its release. Interpret the slope and y-intercept of the line of fit.

Solution :

By plotting these points and drawing the line of best fit, we get

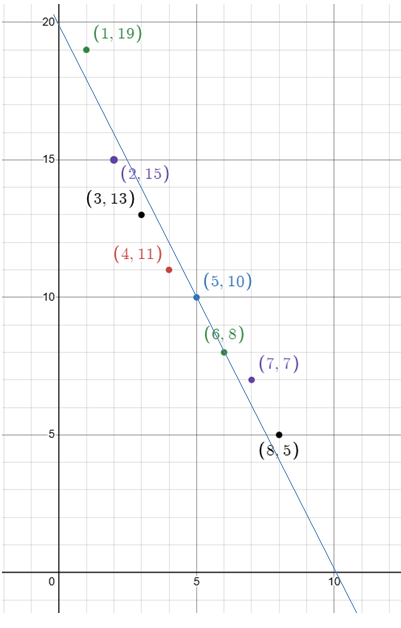
choosing two points on the line of best fit, we get (5, 10) and (6, 8)

Slope (m) = (y₂ - y₁)/(x₂ - x₁)

= (8 - 10) / (6 - 5)

= -2/1

= -2

Slope is -2.

Equation of line of best fit :

y = mx + b

y = -2x + b

The line passes through the point (5, 10)

10 = -2(5) + b

10 = -10 + b

10 + 10 = b

b = 20

Applying the value of b, we get

y = -2x + 20

So, the line of best fit is y = -2x + 20.

Interpreting slope :

For every 1 week sales is decreasing by 2 millions.

Interpreting y-intercept :

At the beginning, the initial number of DVD's is 20 millions.

Problem 2 :

The following data pairs show the monthly income x (in dollars) and the monthly car payment y (in dollars) of six people: (2100, 410), (1650, 315), (1950, 405), (1500, 295), (2250, 440), and (1800, 375).

Write an equation that models the monthly car payment as a function of the monthly income. Interpret the slope and y-intercept of the line of fit.

Solution :

By plotting these points and drawing the line of best fit, we get

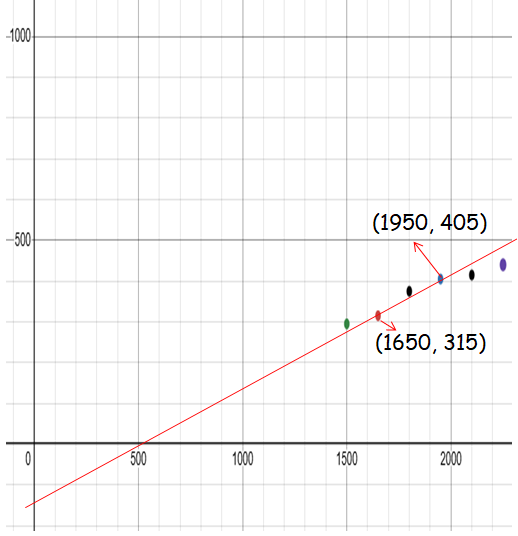
choosing two points on the line of best fit, we get (1650, 315) and (1950, 405)

Slope (m) = (y₂ - y₁)/(x₂ - x₁)

= (405 - 315) / (1950 - 1650)

= 90/300

= 0.3

Slope is 0.3

Equation of line of best fit :

y = mx + b

y = 0.3x + b

The line passes through the point (1650, 315)

315 = 0.3(1650) + b

315 = 495 + b

b = 315 - 495

b = -180

Applying the value of b, we get

y = 0.3x - 180

So, the line of best fit is y = 0.3x - 180

Interpreting slope :

Monthly car payment will increase by 0.3 for 1 dollar increase of monthly income.

Interpreting y-intercept :

At the beginning, the initial monthly payment is 180 dollars.

Problem 3 :

The scatter plot shows the hard drive capacities (in gigabytes) and the prices (in dollars) of 10 laptop

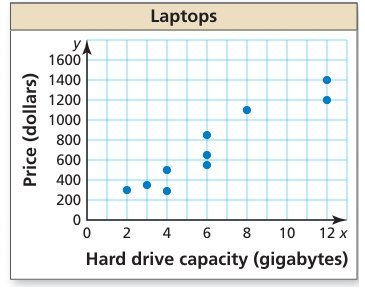
a. What is the price of the laptop with a hard drive capacity of 8 gigabytes?

b. What is the hard drive capacity of the $1200 laptop?

c. What tends to happen to the price as the hard drive capacity increases?

Solution :

a) By observing the scatter plot it is very clear that the price of laptop with a hard drive of capacity 8 gigabytes is 1100 dollars

b) The hard drive capacity of $1200 laptop is 12 gigabytes.

c) It shows the positive relationship between the capacity and rate, when price increases the capacity also increase.

Problem 4 :

The table shows the world birth rates y (number of births per 1000 people) x years since 1960.

a. Write an equation that models the birthrate as a function of the number of years since 1960.

b. Interpret the slope and y-intercept of the line of fit.

Solution :

a) By plotting the points in the graph and drawing line of best fit, we get

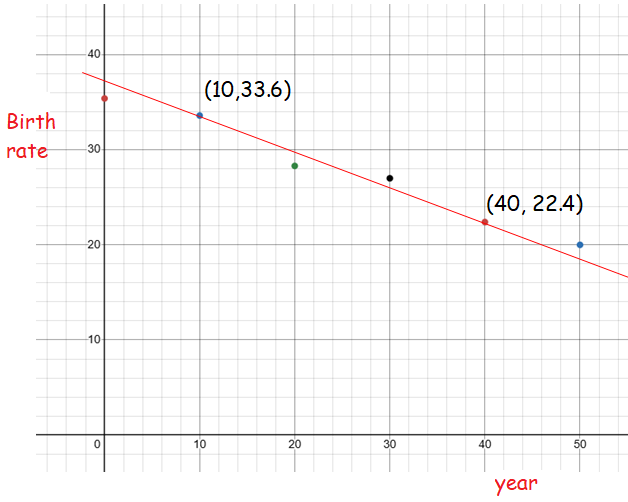
choosing two points on the line of best fit, we get (10, 33.6) and (40, 22.4)

Slope (m) = (y₂ - y₁)/(x₂ - x₁)

= (22.4 - 33.6) / (40 - 10)

= -11.2/30

= -0.37

= -37/100

Slope is -37/100

Equation of line of best fit :

y = mx + b

y = (-37/100)x + b

The line passes through the point (10, 33.6)

33.6 = (-37/100)(10) + b

33.6 = -370/100 + b

33.6 = -3.7 + b

b = 33.6 + 3.7

b = 37.3

Applying the value of b, we get

y = (-37/100)x + 37.3

So, the line of best fit is y = (-37/100)x + b

Interpreting slope :

Birth rate is decreasing 0.37 for every 100 births.

Interpreting y-intercept :

At the year of 1960, the birth rate is 37.3.