PROBLEMS ON REGULAR POLYGON

Problem 1 :

Find the number of sides of a regular polygon which has angles of 150°

Solution :

Sum of the angles of a regular polygon = 150

Let n be the number of sides.

n = 12

So, the number of sides of a required polygon is 12.

Problem 2 :

Is there a regular polygon which has the angle of 158°

Solution :

Here we get the value of n as decimal. So, there is no such regular polygon is having an angle of 158°.

Problem 3 :

For the following regular polygon given below,

find

(i)  Number of sides that the polygon has

(ii) Number of angles

(iii)  Size of each angle.

Solution :

a) Equilateral triangle

Number of sides = 3, number of angles = 3

b) Square

Number of sides = 4, number of angles = 4

c) Pentagon

Number of sides = 5, number of angles = 5

d) Hexagon

Number of sides = 6, number of angles = 6

e) Octagon

Number of sides = 8, number of angles = 8

f) Decagon

Number of sides = 10, number of angles = 10

Problem 4 :

In an equilateral hexagon, four of the exterior angles each have a measure of x°. The other two exterior angles each have a measure of twice the sum of x and 48. Find the measure of each exterior angle.

Solution :

Number of sides of hexagon = 6

Four exterior angle of each = x

The other two exterior angle = 2(x + 48)

Sum of exterior angle of polygon = 360

4x + 2[2(x + 48)] = 360

4x + 2(2x + 96) = 360

4x + 4x + 192 = 360

8x = 360 - 192

8x = 168

x = 21

So, the four angle measures are 21, 21, 21 and 21.

The other angle measure = 2(21 + 48)

= 2(69)

= 138

So, the required angle are 21, 21, 21, 21, 138 and 138.

Problem 5 :

Is the hexagon a regular hexagon. Explain your reasoning.

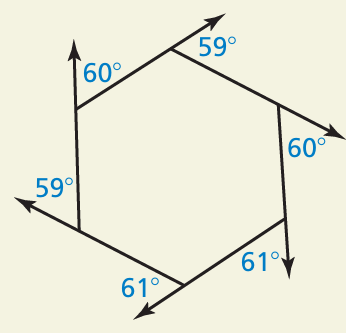
Solution :

If it is regular polygon, then the interior angle should be the same. Since the interior angle measures are not the same, it cannot be a regular hexagon.

Problem 6 :

Describe and correct the error in finding the measure of one exterior angle of a regular pentagon.

Solution :

One interior angle of polygon = (n - 2) (180/n)

Interior angle + exterior angle = 180

Interior angle = 540/number of sides

= 540/5

= 108

108 + exterior angle = 180

exterior angle = 180 - 108

= 72

72 degree is the exterior angle.

Problem 7 :

Find the number of sides for the regular polygon described.

Each interior angle has a measure of 156°.

Solution :

One interior angle of polygon = (n - 2) (180/n)

156 = (n - 2) (180/n)

156n = 180n - 360

180n - 156n = 360

24n = 360

n = 360/24

n = 15

So, the number of sides of a regular polygon is 15.

Problem 8 :

A home plate for a baseball field is shown.

a. Is the polygon regular? Explain your reasoning.

b. Find the measures of ∠C and ∠E.

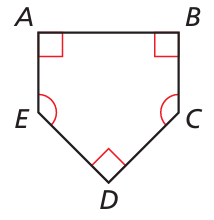
Solution :

a) The polygon is not equilateral or equiangular. So, the polygon is not regular.

b. Find the sum of the measures of the interior angles.

(n − 2) ⋅ 180° = (5 − 2) ⋅ 180° ==> 540°

x° + x° + 90° + 90° + 90° = 540°

2x + 270 = 540

x = 135

So, m∠C = m∠E = 135°.