PROBLEMS ON PROPERTIES OF SQUARE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
What is square ?
A square is a rhombus with four equal angles of 90.
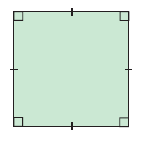
Properties :
- Opposite sides are parallel.
- All sides are equal in length.
- Diagonals bisect each other at right angles.
- Diagonals bisect the angles at each vertex.
- Diagonals are equal in length.
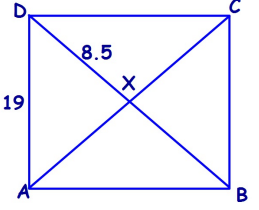
Problem 1 :
The square ABCD, find each length or angle measure.
|
1) BX 2) AX 3) DB 4) AC |
5) AB 6) BC 7) ∠AXB 8) ∠XAB |
Solution :
1) In square, the diagonal will bisect each other. So, BX = 8.5
2) Diagonals are equal, AX = 8.5
3) DB = 2DX, DB = 2(8.5) ==> 17
4) Diagonals are equal. So AC = 17
5) AB = 19
6) BC = 19
7) Diagonals will bisect each other at right angle, ∠AXB = 90
8) Diagonals will bisect the vertex angle, ∠XAB = 45
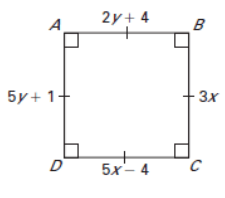
Problem 2 :
Classify the special quadrilateral. Then find the values of x and y.
Solution :
Since all sides are equal and angles at vertex is 90 degree. The given shape is square.
|
AB = DC 5x - 4 = 2y + 4 5x - 2y = 4 + 4 5x - 2y = 8 ------(1) |
AD = BC 5y + 1 = 3x 3x - 5y = 1 3x - 5y = 1 ------(2) |
(1) ⋅ 5 ==> 25x - 10y = 40
(2) ⋅ 2 ==> 6x - 10y = 2
(1) - (2)
19x = 38
x = 38/19
x = 2
By applying x = 1 in (1), we get
5(2) - 2y = 8
10 - 2y = 8
-2y = 8 - 10
-2y = -2
y = 1
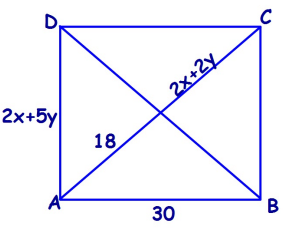
Problem 3 :
For the square ABCD, find the missing values.
|
1) x 2) y |
3) AD 4) DB |
Solution :
Diagonals will bisect each other.
18 = 2x + 2y
Dividing by 2 on both sides.
9 = x + y
x + y = 9 ----(1)
All sides will be equal.
AB = AD
30 = 2x + 5y
2x + 5y = 30 ----(2)
(1) ⋅ 2 - (2) ==> (2x + 2y) - (2x + 5y) = 9 - 30
2y - 5y = -21
-3y = -21
y = 7
Problem 4 :
The diagonals of square DEFG intersect at H. Given that EH = 5, find the indicated measure.
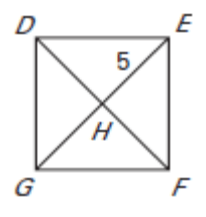
|
1) ∠GHF 2) HF |
3) ∠DGH 4) DE |
Solution :
1) ∠GHF = 90 degree
2) HF = 5
3) ∠DGH = 45 degree
4) In triangle DHE,
(DE)2 = DH2 + HE2
DE2 = 52 + 52
DE2 = 25 + 25
DE = √50
DE = 5√2
Problem 5 :
ABCD is a given rectangle with length as 80 cm and breadth as
60 cm. P, Q, R, S are the mid points of sides AB, BC, CD, DA
respectively. A circular rangoli of radius 10 cm is drawn at the center as shown in figure given below. Find the area of shaded portion.
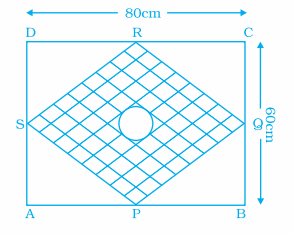
Solution :
DC = 80 cm, DR = 40 cm
DA = 60 cm, DS = 30 cm
In triangle DRS,
RS2 = DR2 + DS2
RS2 = 402 + 302
RS2 = 1600 + 900
RS2 = 2500
RS = 50
RS = PQ = SP = RQ
Area of square PQRS = 2500
Area of circle = πr2
radius = 5 cm
= 3.14 (5)2
= 3.14(25)
= 78.5
Area of shaded portion = 2500 - 78.5
= 1921.5 cm2
Problem 6 :
A large square is made by arranging a small square surrounded by
four congruent rectangles as shown in figure given below. If the perimeter of
each of the rectangle is 16 cm, find the area of the large square.

Solution :
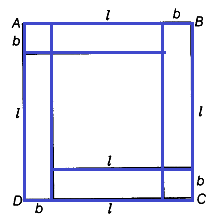
Perimeter of the rectangle = 16 inches
2(l + b) = 16
l + b = 8
Side length of the square = l + b
Area of square = (l + b)2
= 82
= 64
Problem 7 :
ABCD is a square with AB = 15 cm. Find the area of the square BDFE.
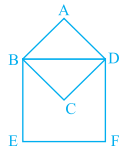
Solution :
ABCD is a square, here BD is the diagonal of the square.
BD2 = AB2 + AD2
BD2 = 152 + 152
BD2 = 450
BD = 15√2
Area of square BDEF = BD2
= (15√2)2
= 225(2)
= 450
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling