PROBLEMS ON POSITION VELOCITY AND ACCELERATION

Problem 1 :

A particle moves along a line so that its position at any time t ≥ 0 is given by the function

s(t) = (1/3) t³ - 3t² + 8t - 5

where s is measured in meters and t is measured in seconds.

a)  Find the instantaneous velocity at any time t.

b)  When is the particle at rest ?

c)  Find the acceleration of the particle at any time t.

d) What is displacement of the particle for the first 3 seconds ?

Solution :

s(t) = (1/3) t³ - 3t² + 8t - 5

a) To find the instantaneous velocity, we have to find the first derivative.

s'(t) = (1/3)(3 t²) - 3(2t) + 8(1) - 0

s'(t) = t² - 6t + 8

b) When v(t) = 0, the particle will be at rest 

v(t) = s'(t) = t² - 6t + 8 = 0

(t - 4)(t - 2) = 0

t = 4 seconds and t = 2 seconds

c)  To find the acceleration, we have to find the second derivative.

a(t) = v'(t) = s''(t) = 2t - 6(1) + 0

a(t) = 2t - 6

d) To find the displacement for first 3 seconds, we have to find s(3) - s(0)

s(3) = (1/3) (3)³ - 3(3)² + 8(3) - 5

= 9 - 27 + 24 - 5

= 33 - 32

= 1

s(0) = (1/3) (0)³ - 3(0)² + 8(0) - 5

= -5

s(3) - s(0) = 1 - (-5)

= 1 + 5

= 6

Problem 2 :

A ball is dropped off a 1200 ft cliff. The height of the ball over is modeled by the function h(t) = 1200 - 16t². Where h is the height of the ball and t is time in seconds.

a)  Find h'(3). Explain what it means.

b)  Find h''(t). Explain what it means.

Solution :

h(t) = 1200 - 16t²

a) Finding h'(3)

h'(t) = 0 - 16(2t)

h'(t) = -32t

h'(3) = -32(3)

h'(3) = -96

At 3 seconds, the ball is falling at the rate of 96 feet/second.

b) Finding h''(3)

h'(t) = -32t

h''(t) = -32(1)

= -32

At 3 seconds, the rate the balls is falling is increasing by 32 feet/ second.

Problem 3 :

The position in meters of a body at time t sec is

s(t) = t³ - 6t² + 9t

Find the body's acceleration each time the velocity is 0.

Solution :

s(t) = t³ - 6t² + 9t

To find the acceleration, we have to find the second derivative.

s'(t) = 3t² - 6(2t) + 9(1)

= 3t² - 6(2t) + 9(1)

s'(t) = 3t² - 12t + 9

When velocity = 0

3t² - 12t + 9 = 0

t² - 4t + 3 = 0

(t - 1)(t - 3) = 0

t = 1 and t = 3

s''(t) = 3(2t) - 12(1) + 0

a(t) = 6t - 12

Problem 4 :

A particle P moves on the number line. The graph s = f(t) shows the position of P as a function of time t.

a)  When is P moving to the left ?

b)  When is P moving to the right ?

c)  When P is rest ?

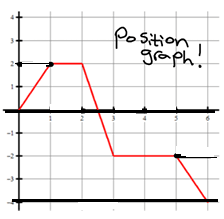
Solution :

a)  In the position graph, in the intervals (2, 3) and (3, 6) the curve is decreasing. So, in the above intervals it is moving left.

b)  At the interval (0, 1), the curve is increasing. So, it is moving in the interval (0, 1) it is moving right.

c)  On the intervals (1, 2) and (3, 5), the curve is horizontal line, so it is in rest in the above intervals.

Problem 4 :

A rock thrown vertically upward from the surface of the moon at the velocity of 32 meters per second reaches a height of s(t) = 32t - 0.8t² meters in t seconds.

a) Find the rock's velocity and acceleration as function of time.

b)  How long did it take the rock to reach its highest point ?

Solution :

a) To find the velocity and acceleration, we have to find the first and second derivative respectively.

s(t) = 32t - 0.8t²

Find the velocity :

s'(t) = 32(1) - 0.8(2t)

s'(t) = 32 - 1.6 t

Finding acceleration :

s''(t) = 0 -1.6(1)

s''(t) = -1.6

b) When the rock reaches the highest point, its velocity will become 0.

32 - 1.6 t = 0

-1.6t = -32

t = 32/1.6

t = 20 seconds

Problem 5 :

The data in the table gives selected values for the velocity in meters per minute, of a particle moving along the x-axis. The velocity v is differentiable function of time t.

a)  At t = 0, is the particle moving left or right ? justify

b)  Is there a time during the time interval 0 ≤ t ≤12 minutes when the particle is at rest ? justify

Solution :

a) At t = 0, the velocity v(t) < 0. Then it is moving left.

b)  Yes, in between 0 to 2 minutes, we see the velocity becomes 0. Then, we decide the particle will be at rest in between the interval 0 to 12 minutes.