PROBLEMS ON MEDIAN OF TRIANGLE

• The median of a triangle is a line segment joining the vertex of the triangle to the mid-point of its opposite side.
• It bisects the opposite side, dividing it into two equal parts.
• The median of a triangle further divides the triangle into two triangles having the same area.

• The centroid R of a triangle is two thirds of the distance from each vertex to the midpoint of the opposite side.

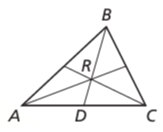
BR = (2/3) BD

Problem 1 :

In the diagram of ABC below, medians AD and BE intersect at point F.

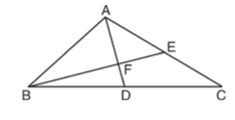
If AF = 6, what is the length of FD?

1) 6     2) 2     3) 3      4) 9

Solution :

Since F is the point of concurrency of medians AD and BE,

AF = (2/3) of AD

6 = (2/3) x AD

6 = 2AD/3

18 = 2AD

AD = 18/2

AD = 9

FD = AD - AF

= 9 - 6

FD = 3

Problem 2 :

In the diagram below of ABC, medians AD, BE, and CF intersect at G.

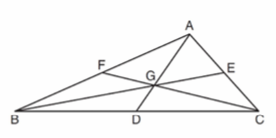
If CF = 24, what is the length of FG?

1) 8   2) 10   3) 12    4) 16

Solution :

Here the medians AD, BE and CF are intersecting at G.

CG = 2/3 of CF

CG = (2/3) x 24

= 2 x 8

CG = 16

Problem 3 :

As shown below, the medians of ABC intersect at D.

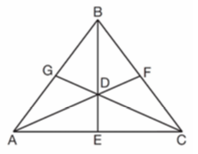
If the length of BE is 12, what is the length of BD?

1) 8    2) 9    3) 3      4) 4

Solution :

BE = 12

BD = (2/3) of BE

BD = (2/3) x 12

BD = 2 x 4

BD = 8

Problem 4 :

In the diagram below of MAR, medians MN, AT, and RH intersect at O.

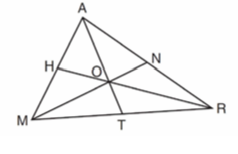
If TO = 10, what is the length of TA?

1) 30    2) 25     3) 20    4) 15

Solution :

TO = (1/3) of TA

10 = (1/3) x TA

TA = 10 x 3

TA = 30

Problem 5 :

In ABC shown below, medians AD, BE, and CF intersect at point R.

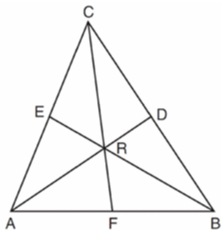
If CR = 24 and RF = 2 x − 6, what is the value of x?

1) 9    2) 12     3) 15      4) 27

Solution :

CR and RF will be in the ratio of 2 : 1

CR / RF = 2/1

24 / (2x - 6) = 2/1

24 = 2(2x - 6)

24 = 4x - 12

24 + 12 = 4x

4x = 36

x = 36/4

x = 9

Problem 6 :

In the diagram of ABC below, Jose found centroid P by constructing the three medians. He measured CF and found it to be 6 inches.

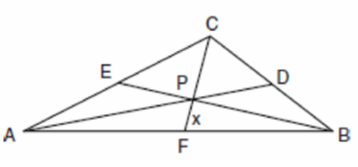
If PF = x, which equation can be used to find x?

1) x +  x =  6    2) 2x +  x =  6

3) 3x + 2x = 6    4) x + (2/3) x = 6

Solution :

CP and PF will be in the ratio of 2 : 1

Since PF is x, then CP would be 2x. Given that CF = 6 inches

CF = PF + CP

6 = x + 2x

Then option 2 is correct.

Problem 7 :

In the diagram below, ABC has medians AX, BY, and CZ that intersect at point P.

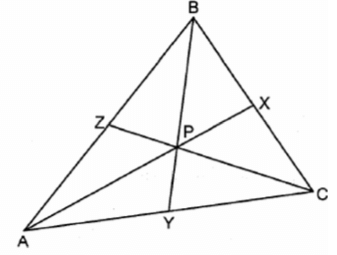
If AB = 26, AC = 28, and PC = 16, what is the perimeter of CZA?

1) 57     2) 65     3) 70       4) 73

Solution :

Here the sides of the triangle are AB, AC and BC. Medians are AX, BY and CZ.

To find perimeter of triangle CZA, we use

= AZ + CZ + AC -----(1)

AB = 26, AZ = 26/2 ==> 13 

AC = 28

CZ = CP + PZ

CP = 16, then PZ = (1/3) of CZ

CZ = 16 + (1/3) of CZ

CZ - (1/3) CZ = 16

2/3 of CZ = 16

CZ = 16 (3/2)

CZ = 24

By applying these values in (1), we get

Perimeter of CZA = 13 + 24 + 28

= 65 units

Problem 8 :

In the diagram below, point P is the centroid of ABC.

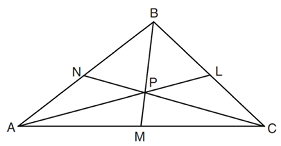
If PM = 2x + 5 and BP = 7x + 4 , what is the length of PM?

1) 9    2) 2     3) 18    4) 27

Solution :

Since P is the centroid of the triangle, this must be the points of intersections of median.

BP : PM = 2 : 1

(7x + 4) : (2x + 5) = 2 : 1

(7x + 4) / (2x + 5) = 2/1

7x + 4 = 2(2x + 5)

7x + 4 = 4x + 10

7x - 4x = 10 - 4

3x = 6

x = 6/3

x = 2

Length of PM = 2x + 5

= 2(2) + 5

= 9 units

Then option (1) is correct.

Problem 9 :

The three medians of a triangle intersect at a point. Which measurements could represent the segments of one of the medians?

1) 2 and 3    2) 3 and 4.5    3) 3 and 6    4) 3 and 9

Solution :

The segments of one of the medians will be in the ratio 2 : 1

Option 3 :

3 and 6 = 3 : 6 ==> 1 : 2

So, option 3 is correct.