PROBLEMS ON LINEAR EQUATIONS FOR CA FOUNDATION

Problem 1 :

If 6 = 2x + 4y, what is the value of x + 2y is 

(a)  2  (b)  3  (c) 6  (d)  8

Solution :

6 = 2x + 4y

Divide by 3 on both sides.

3 = x + 2y

The value of x + 2y is 3.

Problem 2 :

Solve for y in the equation 

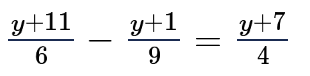
and the value of y is.

(a)  -1  (b)  7   (c)  1   (d) -1/7

Solution :

By finding least common multiple of 6 and 9, we get

3(y+11) - 2(y+1)/18 = (y + 7)/4

(3y + 33 - 2y - 2)/18 = (y + 7)/4

(y + 31)/18 = (y + 7)/4

Multiply by 2 on both sides, we get

(y + 31)/9 = (y + 7)/2

Doing cross multiplication, we get

2(y + 31) = 9(y + 7)

2y + 62 = 9y + 63

2y - 9y = 63 - 62

-7y = 1

Divide by (-7) on both side.

y = -1/7

Problem 3 :

Pick up the correct value x for which

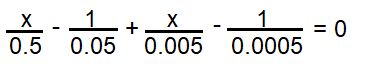
(a)  x = 0   (b) x = 1   (c) x = 10   (d) None of these

Solution :

Multiplying the 1^st fraction by 10/10.

Multiplying the 2^nd fraction by 100/100.

Multiplying the 3^rd fraction by 1000/1000.

Multiplying the 4^th fraction by 10000/10000.

(10x/5) - (100/5) + (1000x/5) - (10000/5) = 0

(10x - 100 + 1000x - 10000)/5 = 0

1010x - 10100 = 5

1010x = 10100

x = 10100/1010

x = 10

Problem 4 :

The denominator of the fraction exceed the numerator by 5 and if 3 be added to both the fraction becomes 3/4. Find the fraction.

(a)  12/17   (b)  15/17   (c)  12/25   (d)  13/29

Solution :

Let the fraction be x/y.

x = numerator, y = denominator.

y = x + 5

The original fraction : x / (x + 5)

After adding 3 in both numerator and denominator, we get

(x + 3) / (x + 5 + 3) = 3/4

(x + 3) / (x + 8) = 3/4

Doing cross multiplication, we get

4(x + 3) = 3(x + 8)

4x + 12 = 3x + 24

x = 12

y = 17

So, the required fraction is 12/17.

Problem 5 :

Three persons Mr. Roy, Mr Paul and Mr. Singh together have $51. Mr Paul has $4 less than Mr Roy and Mr. Singh has got $5 less than Mr.Roy. They have the money as

(a)  (20, 16, 15)   (b)  (15, 20, 16)  (c)  (25, 11, 15)

Solution :

Let R be Roy, P be Paul and S be Singh.

R + P + S = 51 ----(1)

P = R - 4 ---(2)

S = R - 5 ---(3)

Apply the values of R and S in (1), we get

R + R - 4 + R - 5 = 51

3R - 9 = 51

3R = 60

Dividing by 3, we get

R = 20

By applying R in (2) and (3), we get

So, the answer is (R, P, S) ==> (20, 16, 15).

Problem 6 :

A number consists of two digits. The digits in the ten's place is 3 times the digit in the unit's place. If 54 is subtracted from the number the digits are reversed. The number is 

(a)  39   (b)  92  (c) 93  (d)  94

Solution :

Let the two digit number be xy

x - ten's digit and y - unit digit 

x = 3y -----(1)

xy - 54 = yx

10x + 1y - 54 = 10y + 1x 

10x - 1x + 1y - 10y = 54

9x - 9y = 54

x - y = 6 ------(2)

By applying (1) in (2), we get

3y - y = 6

2y = 6

y = 3

By applying y = 3 in (1), we get

x = 3(3) ==> 9

So, the required two digit number is 93.

Problem 7 :

The number consists of two digits, the digit in the ten's place is twice the digit in the unit's place. If 18 be subtracted from the number the digits are reversed. Find the number

(a)  42   (b)  24  (c) 33  (d)  61

Solution :

Let the two digit number be xy

x - ten's digit and y - unit digit

x = 2y ---(1)

xy - 18 = yx

10x + 1y - 18 = 10y + 1x

10x - 1x + 1y - 10y = 18

9x - 9y = 18

x - y = 2 ----(2)

By applying the value of x in (2), we get

2y - y = 2

y = 2

By applying value of y in (1), we get x = 4

So, the required two digit number is 42.

Problem 8 :

Solving 4^x⋅2^y = 128 and 3^3x+2y = 9^xy, we get the following roots.

(a)  7/4, 7/2  (b)  2, 3  (c)  1, 2) (d) 1, 3

Solution :

y = 7 - 2x

3x + 2(7 - 2x) = 2x(7 - 2x)

3x + 14 - 4x = 14x - 4x²

4x² - 4x - 14x + 3x + 14 = 0

4x² - 15x + 14 = 0

(x - 2)(4x - 7) = 0

x = 2 and x = 7/4

So, the required roots are 2 and 3.

Problem 9 :

Solving 9^x = 3^y and 5^x+y+1 = 25^xy, we get the following roots.

(a)  1, 2  (b) 0, 1  (c)  0, 3  (d)  1, 3

Solution :

Applying the value of y in (2)

x + 2x + 1 = 2x(2x)

3x + 1 = 4x²

4x² - 3x - 1 = 0

(x - 1) (4x + 1) = 0

x = 1 and x = -1/4

When x = 1, y = 2(1) ==> 2

When x = -1/4, y = 2(-1/4) ==> -1/2

So, the solution is (1, 2).

Problem 10 :

Solving 9x + 3y - 4z =  3, x + y - z = 0 and 2x - 5y - 4z = -20 the following roots obtained.

(a) 2, 3, 4  (b) 1, 3, 4  (c) 1, 2, 3  (d) None

Solution :

9x + 3y - 4z = 3 ------(1)

x + y - z = 0  --------(2)

2x - 5y - 4z = -20  --------(3)

(1) - 4(2)

9x + 3y - 4z - (4x + 4y - 4z) = 3 + 0

5x - y = 3 -------(4)

2(4) - (3)

4x + 4y - 4z - 2x + 5y + 4z = 0 + 20

2x + 9y = 20 -------(5)

9(4) + (5)

45x - 9y + 2x + 9y = 27 + 20

47x = 47

x = 1

By applying the value of x in (4), we get

So, the solution is (1, 2, 3).

Problem 11 :

One machine can seal 360 packages per hour, and an older machine can seal 140 packages per hour. How many minutes will the two machines working together take to seal a total of 700 packages?

(a) 48  (b) 72  (c) 84  (d) 90

Solution :

Number of packages sealed by the 1^st machine = 360

Number of packages sealed by the 2^nd machine = 140

Number of packages sealed by both machines =  360 + 140

= 500 packages

Working rate of two machines together = 500 package per hour.

60 minute = 500 package

x minutes = 700 package

60 x 700 = 500x

x = 42000/500

x = 84

So, 84 minutes is required to seal 700 packages.

Problem 12 :

The age of a person is 8 years more than thrice the age of the sum of his two grandsons who were twins. After 8 years his age will be 10 years more then twice the sum of the ages of his grandsons. Then the age of the person when twins born is 

(a) 86 years  (b) 73 years  (c) 68 years  (d) 63 years

Solution :

Let x be the age of the sum of his grandsons.

Present age of the person = y

y = 3x + 8  -----(1)

After 8 years :

y + 8 = 2(x + 16) +10

y + 8 = 2x + 32 +10

y + 8 = 2x + 42

y = 2x + 34 -----(2)

(1) = (2)

3x + 8 = 2x + 34

x = 34 - 8

x = 26

y = 3(26) + 8

y = 86

Age of the person when twins born = 86 - 13

= 73 years

So, the age of the person is 73 years.