PROBLEMS ON INTERIOR ANGLES OF A POLYGON

Problem 1 :

Solve for x.

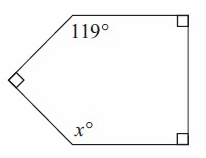
Solution:

Number of sides of the polygon given above = 5

Sum of interior angles of given polygon = (n - 2) × 180°

= (5 - 2) × 180°

= 3 × 180°

= 540°

119° + 90° + 90° + 90° + x° = 540°

389° + x° = 540°

x° = 540° - 389°

x° = 151°

Problem 2 :

Solve for x.

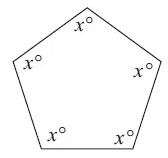
Solution :

Number of sides of the polygon given above = 5

Sum of interior angles of given polygon = (n - 2) × 180°

= (5 - 2) × 180°

= 3 × 180°

= 540°

x° + x° + x° + x° + x° = 540°

 5x° = 540°

x° = 540°/5

 x° = 108°

Problem 3 :

Solve for x.

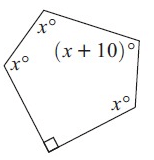
Solution :

Number of sides of the polygon given above = 5

Sum of interior angles of given polygon = (n - 2) × 180°

= (5 - 2) × 180°

= 3 × 180°

= 540°

90° + (x + 10)° + x° + x° + x° = 540°

 100° + 4x° = 540°

4x° = 540° - 100°

 4x° = 440°

x° = 440/4

x° = 110°

Problem 4 :

The sum of the angles of a polygon is 1980°. How many angles has the polygon?

Solution :

Sum of interior angles of a polygon = 1980°

(n - 2) × 180° = 1980°

n - 2 = 1980/180

n - 2 = 11

n = 11 + 2

n = 13

Hence, the polygon has 13 sides.

Problem 5 :

Juan claims to have found a polygon which has angles with a sum of 2500°. Comment on Juan’s finding.

Solution :

Sum of interior angles of a polygon = 2500°

(n - 2) × 180° = 2500°

n - 2 = 2500/180

n - 2 = 13.8

n = 13.8 + 2

n = 15.8

Since the number of sides would not be decimal, there is no such polygon.