PROBLEMS ON INTERIOR AND EXTERIOR ANGLES OF A TRIANGLE

Find the values of the variables :

Problem 1 :

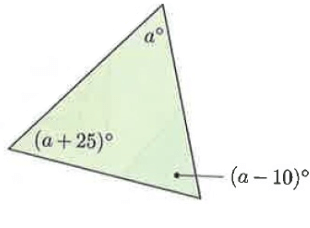
Solution :

The sum of the measures of the interior angles of a triangle is 180°.

a° + (a + 25)° + (a - 10)° = 180°

3a° + 15 = 180°

3a° = 180 - 15

3a° = 165

a° = 165/3

a° = 55

Problem 2 :

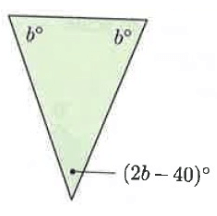
Solution :

The sum of the measures of the interior angles of a triangle is 180°.

b° + b° + (2b - 40)° = 180°

4b° - 40 = 180

4b° = 180 + 40

4b° = 220

b° = 220/4

b° = 55

Problem 3:

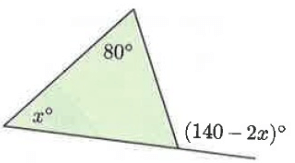
Solution :

Exterior angle = 140 - 2x

Remote interior angles are 80 and x.

Exterior angle = Sum of two remote interior angles

140 - 2x = 80 + x

2x + x = 140 - 80

3x = 60

x = 60/3

x = 20

So, the value of x is 20.

Problem 4 :

Solution :

The sum of the measures of the interior angles of a triangle is 180°.

a° = 55 (corresponding angles)

55° + 48° + b° = 180°

103° + b° = 180°

b° = 180° - 103°

b° = 77

So, the value of a is 55 and b is 77.

Problem 5 :

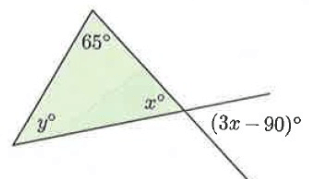
Solution :

3x - 90 = x

3x - x = 90

2x = 90

x° = 45

The sum of the measures of the interior angles of a triangle is 180°.

45° + 65° + y° = 180°

110° + y° = 180°

y° = 180 - 110

y° = 70

So, the value of x is 45 and y is 70.

Problem 6 :

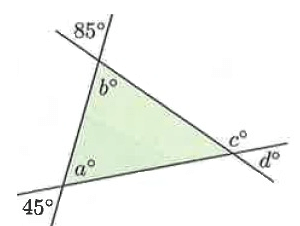
Solution :

a° = 45 and b° = 85

c° = 45 + 85

c° = 130

c° + d° = 180°

130 + d° = 180°

d° = 180 - 130

d° = 50

So, the values of a, b, c and d are 45, 85, 130 and 50 respectively.

Problem 7 :

Two angles of a triangle have equal measures, but the third angle's measure is 36° less than the sum of the other two. Find the measure of each angle of the triangle.

Solution :

Let x be the equal angle measures. y be the third angle and it is 36 less than the sum of other two.

y = 2x - 36

Sum of interior angles of triangle = 180

x + x + y = 180

2x + 2x - 36 = 180

4x = 180 + 36

4x = 216

x = 216/4

x = 54

So, the equal angle measures are 54 and 54.

Other angle = 2(54) - 36

= 108 - 36

= 72

So, the other angle is 72 degree.

Problem 8 :

Find the measures of the angles of an isosceles triangle if the measure of the vertex angle is 40 degrees less than the sum of the measures of the base angles.

Solution :

Since it is isosceles triangle, two of the angle measures will be equal. Let x be the equal angle measures.

The vertex angle = 2x - 40

x + x + 2x - 40 = 180

4x = 180 + 40

4x = 220

x = 220/4

x = 55

2(55) - 40 ==> 110 - 40 ==> 70

so, the required angles are 55, 55 and 70.

Problem 9 :

In a triangle ABC, ∠A = 2x + 7, ∠B = 5x - 15, and ∠C = 6x. What is the value of x and what are the measures of angles A, B, and C?

Solution :

∠A + ∠B + ∠C = 180

2x + 7 + 5x - 15 + 6x = 180

2x + 5x + 6x + 7 - 15 = 180

13x - 8 = 180

13x = 180 + 8

13x = 188

x = 188/13

x = 14.46

∠A = 2x + 7 = 2(14.46) - 7 ==> 21.92

∠B = 5x - 15 = 5(14.46) - 15 ==> 72.3 - 15 ==> 57.3

∠C = 6x ==> 6(14.46) ==> 86.76

So, the required angles are 21.92,  57.3 and 86.76.

Problem 10 :

In a triangle XYZ, ∠X = 37°, ∠Y = 45°, and ∠Z = 3x + 6. What is the value of x and what is the measure of ∠Z?

Solution :

∠X + ∠Y + ∠Z = 180

37 + 45 + 3x + 6 = 180

3x + 88 = 180

3x = 180 - 88

3x = 92

x = 92/3

x = 30.6

Applying the value of x, we get

∠Z = 3(30.6) + 6

= 91.8 + 6

= 97.8

Problem 11 :

Find the angle measures of a triangle if the second angle measures 10 degrees less than twice the first, and the third angle measures 25 degrees more than the second.

Solution :

Let x be the first angle.

Second angle = 2x - 10

Third angle = 2x - 10 + 25

= 2x + 15

x + 2x - 10 + 2x + 15 = 180

5x + 5 = 180

5x = 180 - 5

5x = 175

x = 175/5

x = 35

Second angle = 2(35) - 10 ==> 70 - 10 ==> 60

Third angle = 2(35) + 15 ==> 70 + 15 ==> 85

So, the required angles are 35, 60 and 85.