PROBLEMS ON INCENTER OF TRIANGLE

• The incenter is formed by connecting the three angle bisectors
• The three angle bisectors of a triangle are concurrent at a point equidistant from the sides of a triangle.
• These are the radii of the incircle

Problem 1 :

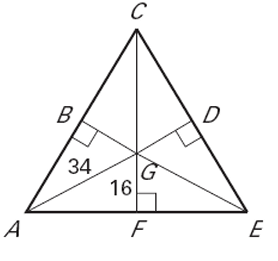
Point G is the incenter of ∆ACE. Find each indicated measure. 

a)  AF     b) BG

Solution :

Here G is the incenter and AC, AE and CE are sides of the triangle.

The distance between incenter and sides of the triangle will be equal. So, BG = GF = DG .

In triangle AGF,

<AFG = 90

AG² = GF² + AF²

34² = 16² + AF²

AF² = 34² - 16²

AF² = 1156 - 256

AF² = 900

AF = √900

AF = 30 and BG = 30

Problem 2 :

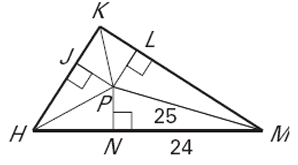
Point P is the incenter of ∆HKM. Find each indicated measure.

a)  PN      b)  JP

Solution :

Since P is the incenter of the triangle, PN = PJ = PL

In triangle PNM,

PM² = PN² + NM²

25² = PN² + 24²

625 - 576 = PN² 

PN² = 49

PN = 7 = JP

Problem 3 :

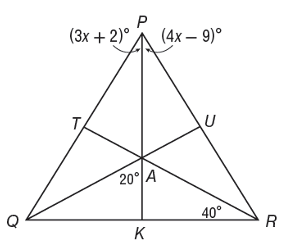
Point A is the incenter of triangle PQR. Find each measure below.

i)  <ARU        ii)   <QPK

Solution :

Since A is the incenter, it must the point of intersection of all angle bisectors of the triangle.

TR is the angle bisector, then <KRA = <ARU = 40 degree

PK is the angle bisector, then <QPK = <KOR

3x + 2 = 4x - 9

3x - 4x = -9 - 2

-x = -11

x = 11

applying the value of x in (3x + 2), we get

= 3(11) + 2

= 33 + 2

= 35

So, <QPK = 35 degree.

Problem 4 :

Find the value of x that makes N the incenter of the triangle.

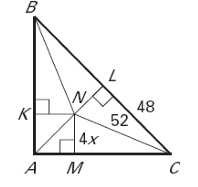
Solution :

Given that MN = 4x(Distance between angle bisector and one side)

MN = NL = KN = 4x

LC = 48, NC = 52, NL = 4x

In triangle NLC :

NC² = NL² + LC²

52² = (4x)² + 48²

2704 = 16x² + 2304

2704 - 2304 = 16x²

16x² = 400

x² = 400/16

x² = 25

x = 5

So, the value of x is 5.

Problem 5 :

Use the diagram below to answer the following questions. Point D is the incenter of ∆𝐴BC. Find the measures of h, k, m, w, x, y, and z.

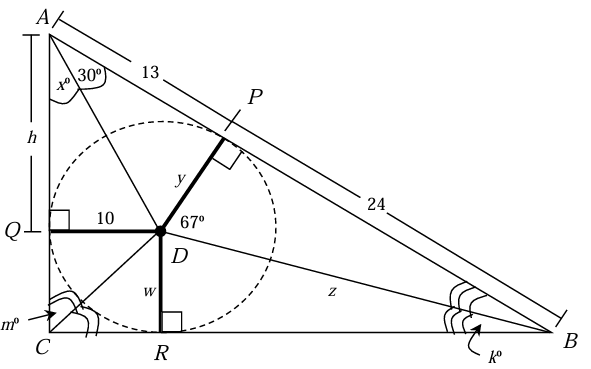
Solution :

Since DA is angle bisector, x = 30°

Since D is the incenter of the circle, QD = DP = DR

y = 10 and w = 10

In triangle PDB,

<PDB + <DBP + <BPD  = 180

67 + k + 90 = 180

157 + k = 180

k = 180 - 157

k = 23

In quadrilateral QDCR,

QD = DR = CR= QC

<DCR = m = 25

In triangle APD,

AD² = DP² + PA²

AD² = 10² + 13²

AD² = 100 + 169

AD² = 269

In triangle AQD,

AD² = AQ² + QD²

269 = h² + 10²

269 - 100 = h² 

h²  = 169

h = 13

In triangle DPB,

DB² = DP² + PB²

z² = y² + 24²

z² = 10² + 24²

z² = 100 + 576

z² = 676

z = √676

z = 26

Problem 6 :

In the diagram below of isosceles triangle ABC, AB ≅ CB and angle bisectors AD, BF, and CE are drawn and intersect at X.

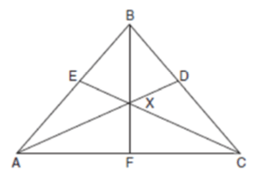
If m ∠BAC = 50°, find m ∠AXC

Solution :

m ∠BAC = 50°

AD is the angle bisector, 

m ∠BAC/2 = 25°

m ∠DAC = 25° and m ∠XCF = 25°

m ∠AXC = 180 - (m ∠XAC + m ∠XCA)

m ∠AXC = 180 - (25 + 25)

m ∠AXC = 180 - 50

m ∠AXC = 130

Problem 7 :

In the diagram below, point B is the incenter of FEC, and EBR, CBD, and FB are drawn.

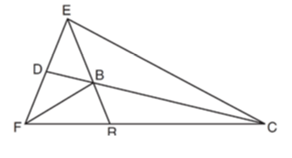
If m ∠FEC = 84 and m ∠ECF = 28, determine and state m ∠BRC.

Solution :

Since B is the incenter, then ER, DC and FB are angle bisectors.

m ∠FEC = 84, then m ∠FEB = <BEC = 42

m ∠ECF = 28, then m ∠ECB = <RCB = 14

In triangle ERC,

<REC + <ERC + <RCE = 180

42 + <ERC + 28 = 180

<ERC + (42 + 28) = 180

<ERC + 70 = 180

<ERC = 180 - 70

<ERC = 110 = <BRC

Problem 8 :

In the diagram below of ABC, CD is the bisector of ∠BCA, AE is the bisector of ∠CAB, and BG is drawn.

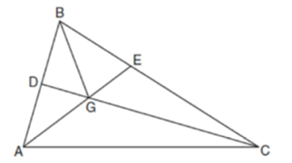
Which statement must be true?

a) DG = EG      b) AG = BG     c) ∠AEB ≅ ∠AEC

d) ∠DBG ≅ ∠EBG

Solution :

Since G is the incenter of the triangle. DG and EG are the distance between incenter and side of the triangle.