PROBLEMS ON GEOMETRY PROPERTIES OF PARALLELOGRAM WITH DIAGONALS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Properties of Parallelogram
In parallelogram, opposite sides are parallel and equal.
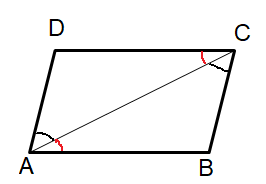
Here diagonal is like a transversal for parallel lines. Then alternate interior angles are equal.
That is,
∠DAC = ∠ACB, ∠DCA = ∠CAB
Since the opposite sides are parallel, we observe the same side interior angles.
∠DAB + ∠ADC = 180
∠DCB + ∠CBA = 180
Conclusion :
- Opposite sides are equal
- Opposite angles are equal
- Sum of consecutive interior angles will be 180 degree.
- Diagonals will bisect each other.
Problem 1 :
Find angle measure ∠YWX.
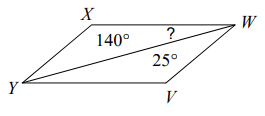
Solution :
Opposite angles are equal.
∠X = 140
∠V = 140
∠V + ∠WYV + ∠VWY = 180
140 + ∠WYV + 25 = 180
165 + ∠WYV = 180
∠WYV = 180 - 165
∠WYV = 15
∠YWX = 15 (alternate interior angles).
Problem 2 :
Find ∠KLJ.
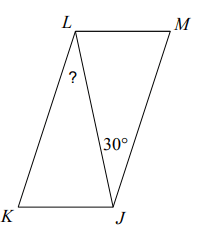
Solution :
In parallelogram, diagonal is a transversal of parallel lines.
∠KLJ = ∠LJM
Alternate interior angles.
∠KLJ = 30
Problem 3 :
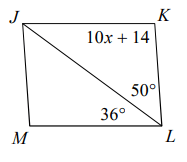
Solution :
∠MLJ = ∠LJK
In the triangle JLK,
∠JLK + ∠LKJ + ∠KJL = 180
50 + 10x + 14 + 36 = 180
10x + 14 + 86 = 180
10x + 100 = 180
10x = 180 - 100
10x = 80
x = 80/10
x = 8
Problem 4 :
FH = 14, QH = 2x - 13
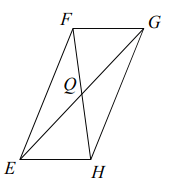
Solution :
In a parallelogram, the diagonals will be equal. Diagonals will bisect each other.
FH = 2QH
14 = 2(2x - 13)
14/2 = 2x - 13
7 = 2x - 13
2x = 7 + 13
2x = 20
x = 20/2
x = 10
Problem 5 :
CJ = 5 + 3x, JE = 2x + 11 and find CJ.
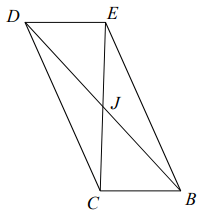
Solution :
CJ = JE
5 + 3x = 2x + 11
5 - 11 = 2x - 3x
-6 = -x
x = 6
Applying the value of x in CJ = 5 + 3x
CJ = 5 + 3(6)
= 5 + 18
CJ = 23
Problem 6 :
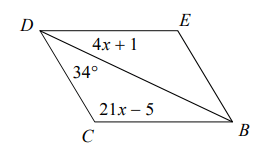
Solution :
∠EDB = ∠DBC
∠DBC = 4x + 1
∠DCB + ∠CBD + ∠CDB = 180
21x - 5 + 4x + 1 + 34 = 180
21x + 4x - 4 + 34 = 180
25x + 30 = 180
25x = 180 - 30
25x = 150
x = 150/25
x = 6
Problem 7 :
Find the indicated measure in ▱LMNQ. Explain your reasoning.
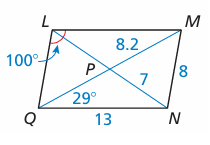
|
a) LM b) LP c) LQ d) MQ |
e) m∠LMN f) m∠NQL g) m∠MNQ h) m∠LMQ |
Solution :
a) LM = 13 (In parallelogram, opposite sides will be equal)
b) LP = 7 (Diagonals will bisect each other)
c) LQ = 8(opposite sides are equal)
d) MQ = 2(8.2) ==> 16.4
e) m∠LMN
m∠QLM + m∠LMN = 180 (cointerior angles)
100 + m∠LMN = 180
m∠LMN = 180 - 100
m∠LMN = 80
f) m∠NQL = 80 (Opposite angles are equal)
g) m∠MNQ = 100 (Opposite angles are equal)
h) m∠LMQ = 29 (Alternate interior angles)
Problem 8 :
For what value of x is quadrilateral CDEF a parallelogram?
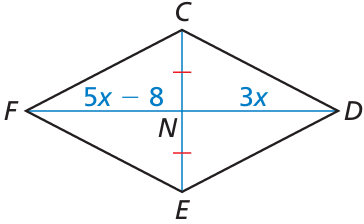
Solution :
Since it is parallelogram, FD and EC are equal. The diagonals will bisect each other. Then,
FN = ND
CN = NE
5x - 8 = 3x
5x - 3x = 8
2x = 8
x = 8/2
x = 4
So, the value of x is 4.
Problem 9 :
For what value of x is quadrilateral MNPQ a parallelogram? Explain your reasoning.
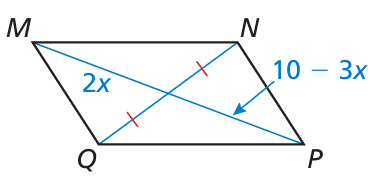
Solution :
2x = 10 - 3x
2x + 3x = 10
5x = 10
x = 10/5
x = 2
So, the value of x is 2.
Problem 10 :
Find the value of x that makes the quadrilateral a parallelogram
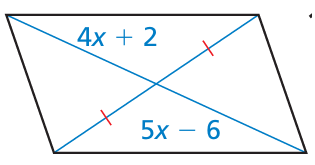
Solution :
Opposite sides will be equal
4x + 2 = 5x - 6
4x - 5x = -6 - 2
-x = -8
x = 8
So, the value of x is 8.
Problem 11 :
What value of x makes the quadrilateral a parallelogram? Explain how you found your answer.
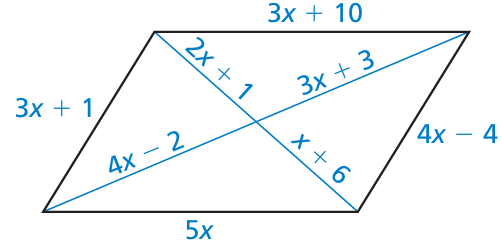
Solution :
4x - 2 = 3x + 3
4x - 3x = 3 + 2
x = 5
So, the value of x is 5.
Problem 12 :
Prove the Parallelogram Diagonals Converse. Given Diagonals JL and KM bisect each other. Prove JKLM is a parallelogram
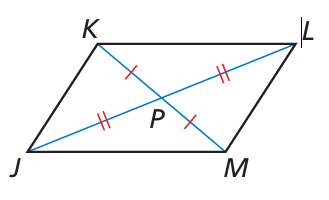
Solution :
JP = PL ------(1)
KP = PM -----(2)
In triangle JPM, KPL
M = KP
JP = PL
<JPM = <KPL (vertical angles)
So, triangle JPM and KPL are congruent, So, JM and KL are equal. Since the opposite sides are equal, then the given shape is a parallelogram.
Problem 13 :
Two adjacent angles of a parallelogram are as 2 : 3. Find the measure of each of its angles.
Solution :
Let the angle measure be 2x and 3x
Since these two are co-interior angles they add upto 180 degree.
2x + 3x = 180
5x = 180
x = 180/5
x = 36
2(36) ==> 72
3(36) ==> 108
So, the adjacent angles are 72 and 108 respectively.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling