PROBLEMS ON EXTERIOR ANGLES OF A QUADRILATERAL

Sum of exterior angle of quadrilateral is 360°.

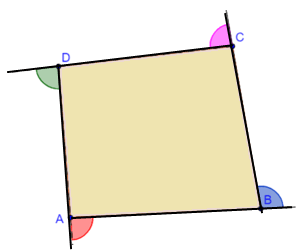
∠A + ∠B + ∠C + ∠D = 360

Find the unknown values in the following :

Problem 1 :

Solution :

∠CDA = 180 - x,  ∠CDE = x

Sum of interior angles of a quadrilateral = 360

118 + 71 + 97 + 180 - x = 360

466 - x = 360

x = 466-360

x = 106

Problem 2 :

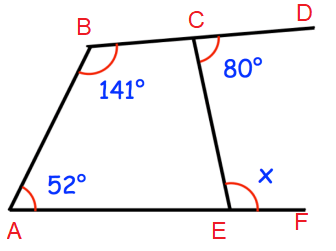
Solution :

∠BCE = 100, ∠CEA = 180 - x

Sum of interior angles of a quadrilateral = 360

52 + 141 + 100 + 180 - x = 360

473 - x = 360

Subtracting 473 on both sides.

-x = 360 - 473

-x = -113

x = 113

Problem 3 :

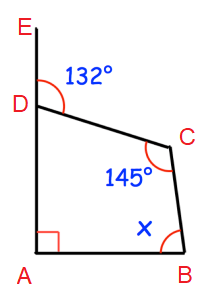
Solution :

∠DAB = 90

∠ADC = 180-132 ==> 48

Sum of interior angles = 360

90 + x + 145 + 48 = 360

283 + x = 360

Subtracting 283 on both sides.

x = 360 - 283

x = 77

Problem 4 :

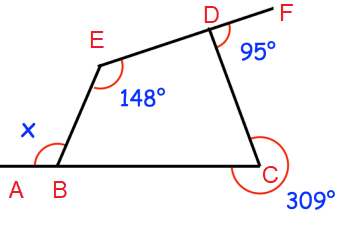
Solution :

Reflexive angle of ∠C = ∠BCD

Sum of interior angle = 360

180 - x + 51 + 85 + 148 = 360

464 - x = 360

Subtracting 464 on both sides.

-x = 360 - 464

-x = -104

x = 104

Problem 5 :

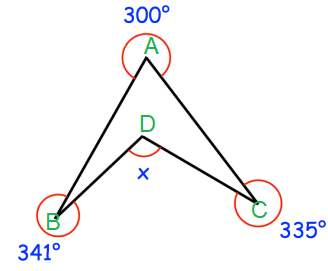
Solution :

Reflexive of ∠B = 360 - 341

∠ABD = 19

Reflexive of ∠C = 360 - 335

∠DCA = 25

Reflexive of ∠A = 360 - 300

∠CAB = 60

Reflexive of ∠BDC = 360 - x

Sum of the interior angles = 360

19 + 25 + 60 + 360 - x = 360

464 - x = 360

Subtracting 464 on both sides.

x = 464 - 360

x = 104

Problem 6 :

Find m∠1 if m∠G = 80, m∠F = 110 and. m∠H = 74.

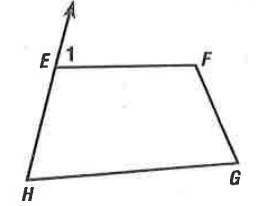
Solution :

m∠G + m∠F + m∠H + m∠HEF = 360

80 + 110 + 74 + m∠HEF = 360

264 + m∠HEF = 360

Subtracting 264 on both sides.

m∠HEF = 360 - 264

m∠HEF = 96

m∠HEF + m∠1 = 180

96 + m∠1 = 180

Subtracting 96 on both sides.

m∠1 = 180 - 96

m∠1 = 94

Problem 7 :

In the given figure, ABCD is a parallelogram. Find the values of x, y, z and p.

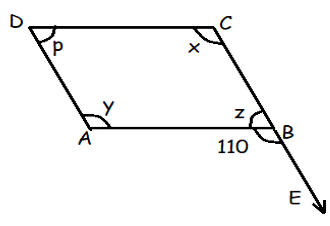
Solution :

∠ABE + z = 180 (linear pair)

110 + z = 180

z = 180 - 110

z = 70

Since it is parallelogram co-interior angles will be add upto 180 degree.

x = 100

Opposite angles will be equal.

y = 100

p = 80

Problem 8 :

Find x + y + z + w in the given figure.

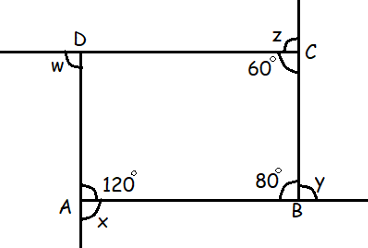
Solution :

x + 120 = 180

x = 180 - 120

x = 60

y + 80 = 180

y = 180 - 80

y = 100

z + 60 = 180

z = 180 - 60

z = 120

∠ADC = 360 - (60 + 80 + 120)

= 360 - 260

= 100

w = 180 - 100

w = 80

x + y + z + w = 60 + 100 + 120 + 80

= 360

So, the value of x + y + z + w is 360.

Problem 9 :

If three angles of a quadrilateral are each equal to 75°, the fourth angle is :

(a) 150°    (b) 135°    (c) 45°        (d) 75°

Solution :

Let x be the fourth angle.

Sum of angles = 360

3(75) + x = 360

225 + x = 360

x = 360 - 225

x = 135

So, option b is correct.

Problem 10 :

 What is the maximum number of obtuse angles that a quadrilateral can have ?

(a) 1           (b) 2          (c) 3            (d) 4

Solution :

A quadrilateral can have a maximum of three obtuse angles because the sum of all interior angles in any quadrilateral is 360°, and if three angles were obtuse (greater than 90°), their sum alone would be over 270°, leaving room for the fourth angle to be acute (less than 90°) to total 360°

Problem 11 :

In the figure, ABCD is a square. If ∠DPC = 80°, then find .

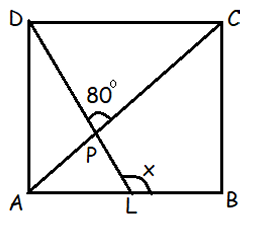
Solution :

∠CPL = 180 - 80 ==> 100

AC is a diagonal, it must be angle bisector. ∠ACB = 45

In quadrilateral CPLB,

∠ACB + ∠CBL + ∠BLP + ∠LPC = 360

45 + 90 + x + 100 = 360

235 + x = 360

x = 360 - 235

x = 125

Problem 12 :

The angle of ∠M, ∠N, ∠O and ∠P of a trapezium MNOP intersect at points W and X respectively. If ∠MPX = 50, ∠NOX = 70, find the measure of the angles a, b, c and d

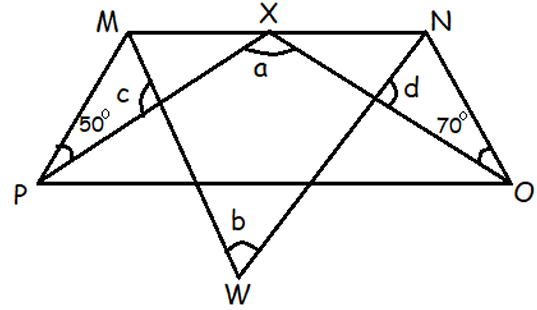
Solution :

In triangle PXO,

∠XPO +  ∠PXO +  ∠XOP = 180

50 + a + 70 = 180

120 + a = 180

a = 180 - 120

a = 60

PO and MN are parallel, then ∠PMN = 180 - 100

= 80

∠PMW = 80/2 ==> 40

∠MNO = 180 - 140

= 40

∠MNW = 40/2 ==> 20

In triangle MNW,

∠MNW + ∠NWM + ∠WMN = 180

20 + b + 40 = 180

b + 60 = 180

b = 180 - 60

b = 120

∠MPX + ∠PMW + c = 180

50 + 40 + c = 180

c = 180 - 90

c = 90

∠WNO + ∠NOX + d = 180

20 + 70 + d = 180

90 + d = 180

d = 180 - 90

d = 90