PROBLEMS ON ESTIMATING THE DERIVATIVES FROM THE TABLE

Approximating a Derivative

If a function f is defined by a table of values, then the approximation values of its derivatives at b can be obtained from the average rate of change using values that are close to b.

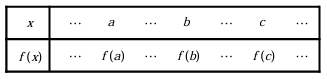
For a < b < c

f'(b) = [f(c) - f(b)] / (c - b)

(or)

f'(b) = [f(b) - f(a)] / (b - a)

(or)

f'(b) = [f(c) - f(a)] / (c - a)

Problem 1 :

The temperature of the water in a coffee cup is a differentiable function F of time t. The table below shows the temperature of coffee in a cup as recorded every 3 minutes over 12 minutes period.

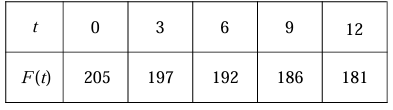
a) Use the data from the table to find an approximation for F'(6) ?

b)  The rate at which the water temperature decreases from 0 ≤ t ≤ 12 is modeled by F(t) = 120 + 85e ^-0.03t degree per minute. Find F'(6) using the given model.

Solution :

a)  F'(6) ≈ F(6) - F(3) / (6 - 3)

= (192 - 197) / 3

= -5/3° F/min 

(or)

F'(6) ≈ F(9) - F(6) / (9 - 6)

= (186 - 192) / 3

= -6/3

= -2° F/min

(or)

 F'(6) ≈ F(9) - F(3) / (9 - 3)

= (186 - 197) / 6

= -11/6° F/min

b)   F(t) = 120 + 85e ^-0.03t

F'(t) = 0 + 85e ^-0.03t (-0.03(1)) 

F'(t) = 85e ^-0.03t (-0.03) 

= -2.55e ^-0.03t

Applying t = 6, we get

F'(6) = -2.55e ^-0.03(6)

= -2.55 e ^-0.18

= -2.55 (2.718) ^-0.18

= -2.129° F/min

Problem 2 :

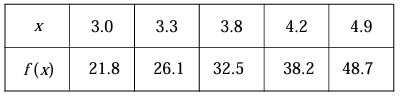
Some values of differentiable function f are shown in the table below. What is the approximation values of f'(3.5) ?

a)  8     b)  10    c)  13    d) 16

Solution :

3.5 lies in the middle of 3.3 and 3.8

f'(3.5) = (f(3.8) - f(3.3)) / (3.8 - 3.3)

= (32.5 - 26.1) / 0.5

= 6.4 / 0.5

= 12.8

So, approximately the answer is 12.8

Problem 3 :

Use the tables to estimate the value of the derivative at the given point.

a) f'(8) = ?

b) f'(3.5) = ?

Solution :

a)  8 lies between 7 and 9.

f'(8) = [f(9) - f(7)] / (9 - 7)

= (902 - 807) / 2

= 95 / 2

= 47.5 visitors per hour

b) 3.5 lies between 3 and 4.

f'(3.5) = [f(4) - f(3)] / (4 - 3)

= (595 - 476) / 1

= 119 / 1

= 119 visitors per hour

Problem 4 :

a) f'(17) = ?

b) = f'(24.5) = ?

Solution :

a) 17 lies in between 11 and 23.

f'(17) = (f(23) - f(11)) / (23 - 11)

= (51 - 71) / 12

= -20 / 12

= -1.666° C per cm

b) 24.5 lies in between 26 and 23.

f'(24.5) = (f(26) - f(23)) / (26 - 23)

= (40 - 51) / 3

= -11 / 3

= -3.667° C per cm

Problem 5 :

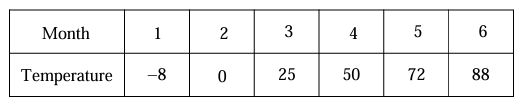
The normal daily maximum temperature F for a certain city is shown in the table above.

a)  Use data in the table to find the average rate of change in temperature from t = 1 to t = 6.

b)  Use the data in the table to estimate the rate of change in maximum temperature at t = 4

c)  The rate at which the maximum temperature changes from 1 ≤ t ≤ 6 is modeled by  F(t) = 40 - 52 sin (πt/6 - 5) degree per minute. Find F'(4) using the given model.

Solution :

a)  Average rate of change :

= f(b) - f(a) / (b - a)

t = 1 and t = 6

= [f(6) - f(1)] / (6 - 1)

= (88 - (-8)) / 7

= (88 + 8) / 7

= 96/7

= 13.71

b) Rate of change at t = 4

= f(4) - f(3) / (4 - 3)

= (50 - 25) / 1

= 25

c)   F(t) = 40 - 52 sin (πt/6 - 5)

F'(t) = 0 - 52 sin (πt/6 - 5) (π/6 - 0)

At t = 4

F'(4) = - 52 sin (π4/6 - 5) (π/6)

F'(4) = - 52 sin (2π/3 - 5) (π/6)