Problems on Corresponding Angles

When two lines are parallel lines are cut by a third line, the angles in corresponding positions are equal in size.

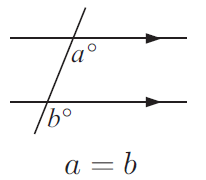
Find the unknown angle measures.

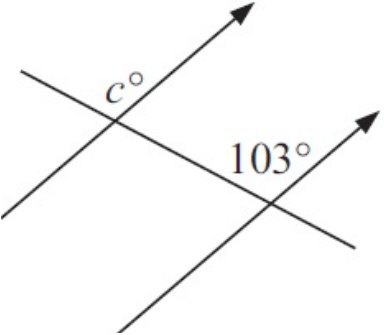
Problem 1 :

Solution :

Angle c and 103 are in corresponding positions. So, they are equal.

∠c = 103

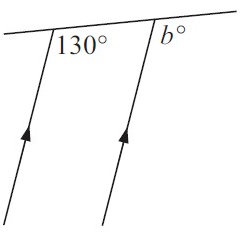
Problem 2 :

Solution :

Angle 130 and b are in corresponding positions. So, they are equal.

∠b = 103

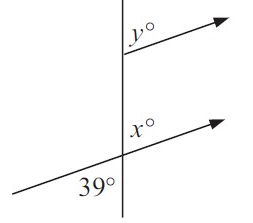
Problem 3 :

Solution :

Angles y and x are in corresponding positions.

y = x

x and 39° are vertically opposite angles.

x = 39° (Vertically opposite angles)

y = 39° (Corresponding angles)

Problem 4 :

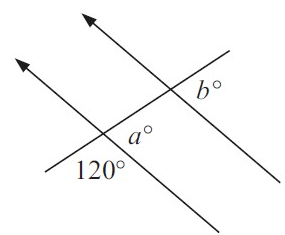
Solution :

120 and a° are linear pair.

120 + a = 180

a = 180 - 120

a = 60

a and b are in corresponding positions.

a = b = 60

Problem 5 :

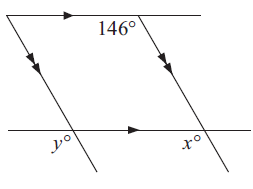
Solution :

Angles x° and 146° are in corresponding positions.

x = 146°

Angles x and y are in corresponding positions.

x = y = 146°

Problem 6 :

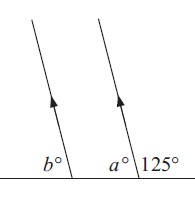
Solution :

Angles a and 125 are linear pairs.

a + 125 = 180

a = 180 - 125

a = 55°

b and a are in corresponding positions.

a = b = 55°

Problem 7 :

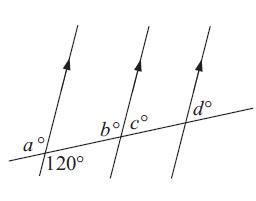
Solution :

a = 120°, because they are vertically opposite angles.

a = b, because they are corresponding angles.

b and c are linear pair. So,

b + c = 180

120 + c = 180

c = 180 - 120

c = 60°

Again c and d are corresponding angles. So, c = d = 60°

Problem 8 :

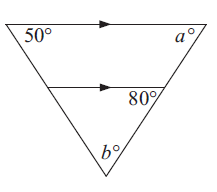
Solution :

In the triangle given above,

a and 80° corresponding angles.

So, a = 80°

In the triangle, the sum of interior angles of triangle is 180°.

50 + a + b = 180

50 + 80 + b = 180

130 + b = 180

b =180 - 130

b = 50

Problem 9 :

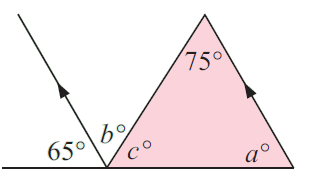
Solution :

Angles a and 65° are in corresponding positions.

a = 65°

In the triangle,

75 + a + c = 180

75 + 65 + c = 180

140 + c = 180

c = 180 - 140

c = 40

65 + b + c = 180 (linear pair)

65 + b + 40 = 180

105 + b = 180

b = 180 - 105

b = 75

Problem 10 :

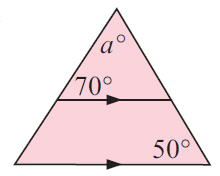
Solution :

We have two parallel sides, so one of the angle measure inside the small triangle is 50.

70 + a + 50 = 180

120 + a = 180

a = 180 - 120

a = 60