PROBLEMS ON CONICS PARABOLA ELLIPSE AND HYPERBOLA

Problem 1 :

Tangents are drawn to the hyperbola 

parallel to he straight line 2x - y = 1. One of the points of contact of tangents on the hyperbola is 

Solution :

Point of contact of the hyperbola :

Problem 2 :

The equation of the circle passing through the foci of the ellipse 

having center at (0, 3) is

a)  x² + y² - 6y - 7 = 0         b)  x² + y² - 6y + 7 = 0

c)  x² + y² - 6y - 5 = 0         d)  x² + y² - 6y + 5 = 0

Solution :

Foci are (√7, 0) and (-√7,0)

Distance between center (0, 3) and (√7, 0) = radius

radius = √(0-√7)² + (0-3)²

= √(7 + 9)

= √16

radius = 4

Equation of circle :

(x - h)² + (y - k)² = r²

(x - 0)² + (y - 3)² = 4²

x²+ y² - 6y + 9 = 16

x²+ y² - 6y + 9 - 16 = 0

x²+ y² - 6y - 7 = 0

Problem 3 :

Consider an ellipse whose center is of the origin and its major axis is along x-axis. If its eccentricity is 3/5 and the distance between its foci is 6, then the area of the quadrilateral in the ellipse with diagonals as major and minor axis of the ellipse is 

a)  8         b)  32    c) 80         d)  40

Solution :

e = 3/5

Distance between foci = 6

2ae = 6

ae = 3

a(3/5) = 3

a = 5

a² = 25

b² = a²(1 - e²)

= 25(1 - (3/5)²)

= 25(1 - (9/25))

= 25[(25-9)/25]

b² = 16

a² = 25 and b² = 16

The ellipse is symmetric about x-axis. Diagonals are major and minor axis.

Length of major axis = 2a ==> 2(5)  ==> 10

Length of minor axis = 2b ==> 2(4)  ==> 8

Area of quadrilateral = (1/2) x d₁ x d₂

= (1/2) x 10 x 8

= 40

Problem 4 :

Area of the greatest rectangle inscribed in the ellipse 

a) 2ab       b) ab     c)  √ab       d)  a/b

Solution :

Area of the rectangle = length x width

length of major axis = 2a = length of the rectangle

length of minor axis = 2b

Half the length of minor axis = b = width of the rectangle

Area = 2a (b) ==> 2ab

Problem 5 :

An ellipse has OB as semi minor axes, F and F' its foci and the angle FBF' is a right angle then the eccentricity of ellipse is 

a) 1/√2       b) 1/2     c)  1/4       d)  1/√3

Solution :

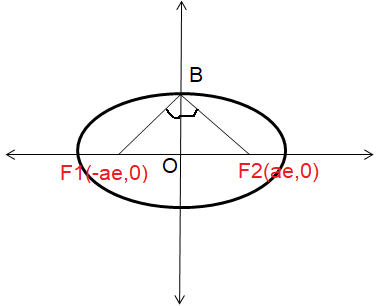
OB = b, OF1 = ae = b

In the right triangle F₁BF₂

(F₁F₂)² = (F₁B)² + (F₂B)²

Problem 6 :

The eccentricity of the ellipse (x - 3) + (y - 4)² = y²/9

a) √3/2       b) 1/3     c)  1/3√2      d)  1/√3

Solution :

Problem 7 :

If the two tangents from a point P to the parabola y² = 4x are at right angles then locus P is 

a) 2x + 1 = 0       b) x = -1     c)  2x - 1 = 0      d)  x = 1

Solution :

The required locus is at x = -1

Problem 8 :

The locus of a point whose distance from (-2, 0) is 2/3 times its distance from the line x = -9/2 is

a) a parabola       b) hyperbola     c)  ellipse      d)  circle

Solution :

Let P the point of locus. P(h, k) and Q(-2, 0)

Distance from the line x = -9/2

So, it is ellipse.

Problem 9 :

The value of m for which the line y = mx + 2√5 touches the hyperbola 16x² - 9y² = 144 are the roots of x² - (a + b)x - 4 = 0, then the value of (a + b) is

a) 2       b) 4   c)  9      d)  -2

Solution :