PROBLEMS ON CONIC SECTIONS WORKSHEET

Problem 1 :

A hyperbolic mirror can be used to take panoramic photos, if the camera is pointed toward the mirror with the lens at one focus of the hyperbola. Write the equation of the hyperbola that can be used to model a mirror that has a vertex 5 inches from the center of the hyperbola and a focus 1 inch in front of the surface of the mirror. Assume the mirror has a horizontal transverse axis and the hyperbola centered at (0, 0).

Solution

Problem 2 :

Skips designs tracks for amusement park rides. For a new design, the track will be elliptical. If the ellipse is placed on a large coordinate grid with center at (0, 0). The equation

models the path of the track . The units are given in yards. How long is the major axis of the track.? Explain how you find the distance.

Solution

Problem 3 :

The equation of parabola is

24y = (x - 2)² - 48

identify the vertex, focus and directrix of the parabola.

Solution

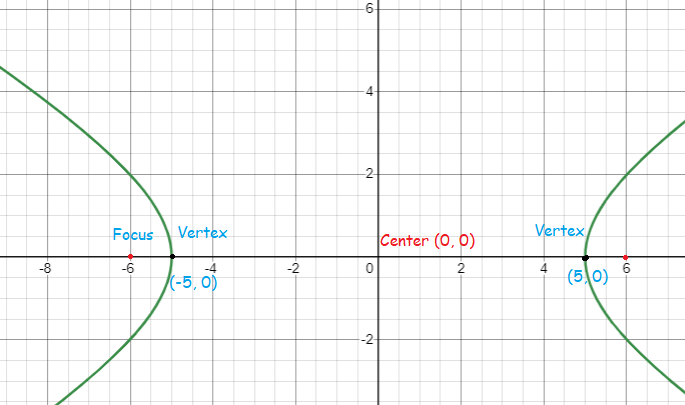
Problem 4 :

The hyperbola has vertices (±4, 0) and focus (5, 0). What is the standard form equation of the hyperbola ?

Solution

Problem 5 :

State the vertices, foci, and asymptotes of the hyperbola with the equation 

20x² - 25y² = 100

Solution

Problem 6 :

Find the equation that models the path of a satellite if its path is a hyperbola, a = 45000 km and c = 71000. Assume that the center of the hyperbola is the origin and the transverse axis is horizontal.

Solution

Answer Key

1)  x²/25 - y²/9 = 1

2)  Length of major axis = 180 units.

3)  

Center : (h, k) ==> (2, -2)

Focus : (h, a) ==> (2, 1/96)

Equation of directrix : y = -a

y = -1/96

4)

5)  

Center :

(0, 0)

Vertices :

A (√5, 0) and A' (-√5, 0)

Foci :

F₁(3, 0) and F₂ (-3, 0)

Asymptotes :

x = (2/√5)  and x = -(2/√5)

6)  (x² / 2025000000) - (y² / 3016000000)= 1