PROBLEMS ON COMPLEMENTARY AND SUPPLEMENTARY ANGLES

Find the values of unknowns :

Problem 1 :

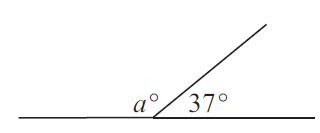
Solution :

In the picture the above angles are linear pairs.

a + 37 = 180

a = 180 - 37

a = 143

Problem 2 :

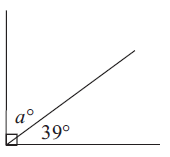
Solution :

Since the angles a and 39 are complementary, sum of those angles will be 90°.

a + 39 = 90

a = 90 - 39

a = 51°

Problem 3 :

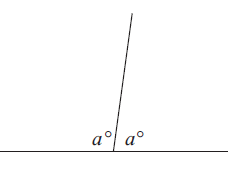
Solution :

In the picture the above angles are linear pairs.

a + a = 180

2a = 180

a = 180/2

a = 90

Problem 4 :

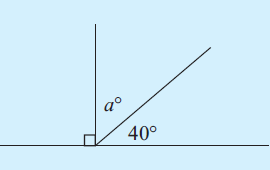
Solution :

From the picture, it is clear

90 + a + 40 = 180

130 + a = 180

a = 180 - 130

a = 50

Problem 5 :

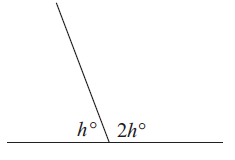
Solution :

h and 2h are supplementary.

h + 2h = 180

3h = 180

Divide by 3, we get

h = 180/3

h = 60

Problem 6 :

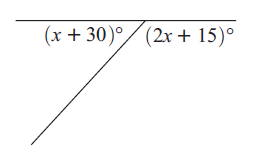
Solution :

x + 30 and 2x + 15 are supplementary.

x + 30 + 2x + 15 = 180

3x + 45 = 180

Subtracting 45

3x = 180 - 45

3x = 135

Divide by 3

x = 135/3

x = 45

Problem 7 :

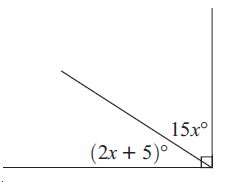
Solution :

2x + 5 and 15x are complementary.

2x + 5 + 15x = 90

17x + 5 = 90

Subtracting 5 on both sides.

17x = 90 - 5

17x = 85

Dividing by 17 on both sides.

x = 85/17

x = 5

Problem 8 :

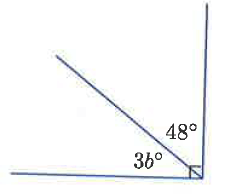
Solution :

3b and 48 are complementary.

3b + 48 = 90

Subtracting 48 on both sides.

3b = 90 - 48

3b = 42

Dividing by 3, we get

b = 42/3

b = 14

Problem 9 :

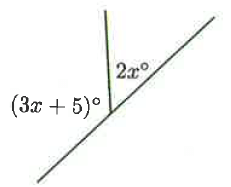
Solution :

3x + 5 and 2x are supplementary.

3x + 5 + 2x = 180

5x + 5 = 180

Subtracting 5 on both sides.

5x = 180 - 5

5x = 175

Divide by 5 on both sides.

x = 175/5

x = 35

Problem 10 :

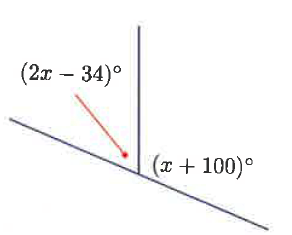
Solution :

2x - 34 and x + 100 are supplementary.

2x - 34 + x + 100 = 180

3x + 66 = 180

Subtracting 66 on both sides.

3x = 180 - 66

3x = 114

Dividing by 3 on both sides.

x = 114/3

x = 38

Problem 11 :

∠UVW and ∠XYZ are complementary angles, m∠UVW = (x − 10)°, and m∠XYZ  = (4x − 10)°.

Solution :

If two angles are complementary, then they add upto 90 degree.

m∠UVW + m∠XYZ = 90

x - 10 + 4x - 10 = 90

5x - 20 = 90

5x = 90 + 20

5x = 110

x = 110/5

x = 22

Applying the value of x in m∠UVW = (x − 10)°

m∠UVW = (22 - 10)°

= 12°

m∠XYZ = 90 - 12

= 78

Problem 12 :

∠EFG and ∠LMN are supplementary angles, m∠EFG = (3x + 17)°, and m∠LMN = ( (1/2)  x − 5)°.

Solution :

If two angles are supplementary, then they add upto 180 degree.

m∠EFG + m∠LMN = 180

3x + 17 + (1/2) x − 5 = 180

3x + (x/2) + 12  = 180

(6x+x)/2 = 180 - 12

7x/2 = 168

7x = 168(2)

x = 336/7

x = 48

Applying the value of x in m∠EFG = 3x + 17

= 3(48) + 17

= 144 + 17

= 161

m∠LMN = 180 - 161

= 19

Problem 13 :

Use the figure.

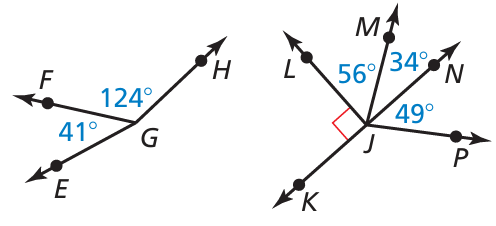
a) Name a pair of adjacent complementary angles.

b) Name a pair of adjacent supplementary angles.

c) Name a pair of nonadjacent complementary angles.

d) Name a pair of nonadjacent supplementary angles.

Solution :

a) ∠LJM and ∠MJN are adjacent angles.  

∠LJM + ∠MJN = 56 + 34

= 90

∠LJM and ∠MJN are adjacent and complementary angles.

b) ∠KJL and ∠LJN are adjacent angles.

∠KJL + ∠LJN = 90 + (56 + 34)

= 90 + 90

= 180

So, ∠KJL and ∠LJN adjacent supplementary angles.

c) ∠MJN and ∠NJP are adjacent angles. They are not complementary. 

∠MJN + ∠NJP = 34 + 49

= 83 (not equal to 90 degree)

Since the sum of the angles is not equal to 90 degree, they are not complementary. So, ∠MJN and ∠NJP are adjacent and non complementary angles.

d) ∠FJH and ∠LJM are non adjacent, but they add upto 180. They they are non adjacent and supplementary angles.

Problem 14 :

Find the measure of each angle.

a)Two angles form a linear pair. The measure of one angle is twice the measure of the other angle.

b) Two angles form a linear pair. The measure of one angle is 1/3 the measure of the other angle.

Solution :

a) Let x b the one angle measure.

The other angle be 2x.

Linear pairs add upto 180 degree. Then,

x + 2x = 180

3x = 180

x = 180/3

x = 60

2x ==> 2(60) ==> 120

So, the required angles are 60 and 120 degree.

b) Let x be the other angle, then one angle will be 1/3 of x

x + x/3 = 180

(3x + x)/3 = 180

4x = 180(3)

x = 180(3)/4

x = 135