PROBLEMS ON CIRCLE FOR SAT

Problem 1 :

If the area of a circle is 64π, then the circumference of the circle is

(A) 8π      (B) 16π    (C) 32 π      (D) 64 π     (E) 128π

Solution :

Area of circle = 64π

πr² = 64π

r² = 64π/π

r² = 64

r = 8

Circumference of circle = 2πr

= 2π(8)

= 16π

Problem 2 :

If the minute hand of a clock moves 45 degrees, how many minutes of time have passed?

(A) 6      (B) 7.5      (C) 15      (D) 30     (E) 36.5

Solution :

Angle between 12 to 3 is 90 degree.

To cross 15 minutes, the clock will cross 90 degree. So half of 15 minutes = 7.5 minutes.

Problem 3 :

If the circumference of a circle is 1, what is the radius of the circle?

(A) 1/2π      (B) 1/π      (C) 1/2      (D) π/2    (E) π

Solution :

circumference of a circle = 1

2π r = 1

r = 1/2π

So, radius of the circle is 1/2π.

Problem 4 :

In the figure below, the ratio of the circumference of circle to the length of arc ADC is 8:1. What is the value of ?

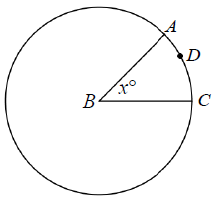
Solution :

Circumference of circle : Length of arc ADC = 8 : 1

2πr : (θ/360)2πr = 8 : 1

1 :  (x/360) = 8 : 1

360/x = 8/1

8x = 360

x = 360/8

x = 45

Problem 5 :

In the figure above, if the area of the circle with center is 100π and CA has a length of 6, what is the length of AB ?

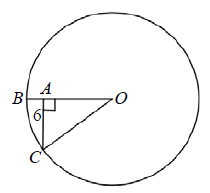
(A) 2        (B) 3     (C) 4     (D) 5     (E) 6

Solution :

Area of the circle = 100π

πr² = 100π

r² = 100

r = 10 = BO = OC

In triangle AOC,

OC² = AO² + AC²

10² = AO² + 6²

100 - 36 = AO²

AO² = 64

AO = 8

BO = AB + AO

10 = AB + 8

AB = 10 - 8

AB = 2

Length of AB is 2 units.

Problem 6 :

In the figure below, is the center of the circle. If the area of triangle XOY is 25, what is the area of the circle?

(A) 25 π     (B) 25 π√2     (C) 50π     (D) 50π√3    (E) 625

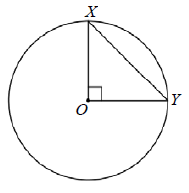
Solution :

Area of triangle = 25

(1/2) • base • height = 25

(1/2) • OX • OY = 25

OX = OY = Radius

(1/2) • (OX)² = 25

(OX)² = 25(2)

OX = 5√2

Area of circle = π(50)

= 50π

Problem 7 :

Each of the 3 shaded regions above is a semicircle. If AB = 4, CD = 2 BC and BC = 2 AB, then the area of the entire shaded figure is 

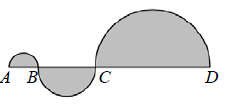
(A) 28 π     (B) 42 π     (C) 84π     (D) 96π    (E) 168π

Solution :

AB = 4 (diameter of the semicircle)

BC = 2AB ==> 2(4) ==> 8 (diameter of the second semicircle)

CD = 2BC ==> 2(8) ==> 16 (diameter of the third semicircle)

Area of circle having diameter AB = π(2)²   ----(1)

Area of circle having diameter BC = π(4)²  ----(2)

Area of circle having diameter CD = π(8)²  ----(3)

(1) + (2) + (3)

= π(2)² + π(4)² + π(8)²

= π(4 + 16 + 64)

= 84π

Problem 8 :

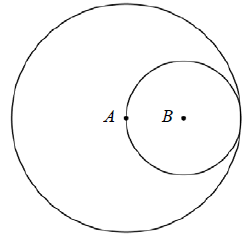
In the diagram below, if the circle with center A has an area of 72π, what is the area of the circle with center B?

(A) 18π   (B) 24π     (C) 30π      (D) 36π      (E) 48π

Solution :

Area of circle with center A = πr²

πr² = 72π

r² = 72

r = 6√2

Radius of the circle with center A = Diameter of the with center B

 6√2 = 2(radius of circle with center B)

Radius of circle with center B = 3√2

Area of circle with center B = π(3√2)²

= 9 (2)π

= 18π

Problem 9 :

If the diameter of a circle increases by 50 percent, by what percent will the area of the circle increase?

(A) 25%     (B) 50%     (C) 100%    (D) 125%    (E) 225%

Solution :

Diameter of the old circle = D(100%)

Diameter of new circle after this increment = 150% of D.

Radius of new circle = 150% of r

Area of new circle = πr²

= π(1.50r)²

= 2.25πr²

= 225% of πr²

Percentage increase of new circle is 225%.

Problem 10 :

If an arc with a length of 12 π is 3/4 of circumference of a circle, what is the shortest distance between the endpoints of the arc?

(A) 4     (B) 4√2   (C) 8 π    (D) 8√2     (E) 16

Solution :

Length of arc = 12π

12π = 3/4 of 2πr

12π(4/3) (1/2π) = r

r = 8

Distance between endpoint of the circle = length of arc

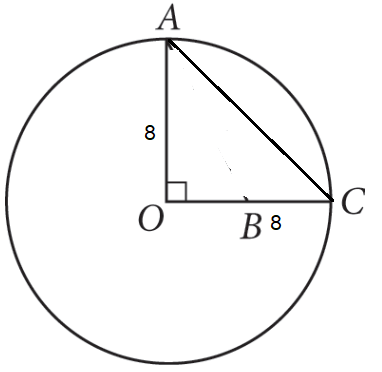
Distance between AC = √8² + 8²

= √128

= 8√2

Problem 11 :

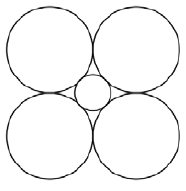
The total area of the four equal circles in the figure above is 36π, and the circles are all tangent to one another. What is the diameter of the small circle?

Solution :

All four circles are having same radius.

Area of circles = 36π

4πr² = 36π

r² = 9

r = 3

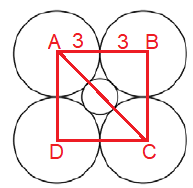
In the square ABCD, finding diagonal AC

AC = √6² + 6²

AC = √36 + 36

AC = √72

AC = 6√2

Diameter of the small circle = 6√2 - 6