PROBLEMS ON AREA AND PERIMETER OF A SQUARE

Problem 1 :

The area of a square and rectangle are equal. If the side of the square is 15 cm and the breadth of the rectangle 10 cm, find the length of the rectangle and its perimeter.

Solution :

Area of a square = Area of rectangle

a² = Length × breadth

Here a = 15 cm, and breadth = 10 cm

15² = Length × 10

225/10 = Length

22.5 = Length

Length of the rectangle = 22.5 cm

Perimeter of the rectangle = 2(Length + breadth)

= 2(22.5 + 10)

= 2(32.5)

Perimeter = 65

Problem 2 :

A wire is in the shape of a rectangle whose width is 12 cm is bent to form a square of side 17 cm. Find the rectangle length and also find which shape encloses more area.

Solution :

Perimeter of a square = 4 side

Here side of the square = 17cm

Perimeter = 4(17)

P = 68 cm

Area of the square = a² 

= 17 × 17

Area = 289 cm²

Perimeter of square = Perimeter of rectangle

Because they are made by the same wire.

Perimeter of rectangle = 68 m

Perimeter of the rectangle = 2(Length + width)

Here width = 12 cm

68 = 2(L + 12)

68 = 2L + 24

68 - 24 = 2L

44 = 2L

Length = 22 cm

Area of the rectangle = Length × width

= 22 × 12

Area = 264 cm²

289 cm² > 264 cm²

Area of the square > Area of the rectangle

So, the area of the square is greater than the area of the rectangle.

Problem 3 :

The area of a square field is 49 hectares. Find the cost of fencing field with a wire at the rate of $5 per m.

Solution :

Area of the square field = 49 hectares.

1 hectare = 10000 square meter.

49 hectares = 49 × 10000

Area = 490000 m²

Area of the square = a² 

490000 = a²

a = √490000

a = 700 m

So, the side of the square field is 700 m.

Now, we find the fencing field (Perimeter).

Perimeter of a square = 4 side

= 4(700)

P = 2800 m

Cost of fencing 1 m = $5

Cost of fencing 2800 m = $5

=  2800 × 5

= $14000

Problem 4 :

How many square tiles of side 6cm will be needed to fit in a square floor of a bathroom of side 600 cm. Find the cost of tiling at the rate of $65 per tile.

Solution :

Side of the square tile = 6 cm

Area of the square = a² 

= 6 × 6

Area = 36 cm²

Side of the square floor = 600 cm

Area of the square = a² 

= 600 × 600

Area = 360000 cm²

Number of tiles required = Area of the square floor/Area of tiles

= 360000/36

= 10000 tiles

Cost of 1 tile = $65

Cost of 10000 tile = 10000 × 65

= $650000

Problem 5 :

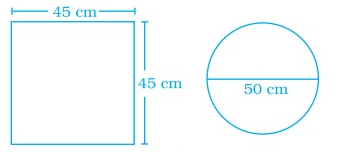
Pizza factory has come out with two kinds of pizza. A square pizza of side 45 cm costs ₹ 150 and a circular pizza of diameter 50 cm costs  ₹ 160. Which pizza is a better deal?

Solution :

Side of the square pizza = 45 cm

Area of the square pizza = a² 

= 45 × 45

= 2025 cm²

Diameter of the circular pizza = 50 cm.

Radius (r) = 50/2

r = 25 cm

Area of the circular pizza = πr²

= 22/7 × 25 × 25

= (13750)/7

Area = 1964.28 cm²

Cost of 1 cm² square pizza = ₹ 150

Cost of 2025 cm² square pizza = (2025)/150

= ₹ 13.5

Cost of 1 cm² circular pizza = ₹ 160

Cost of 1964.28 cm² circular pizza = (1964.28)/160

= ₹ 12.27

So, the circular pizza is a better deal.

Problem 6 :

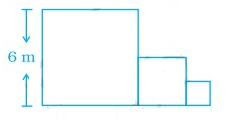
Three squares are attached to each other as shown. Each square is attached at the midpoint of the side of the square to its right. Find the perimeter of the complete figure.

Solution :

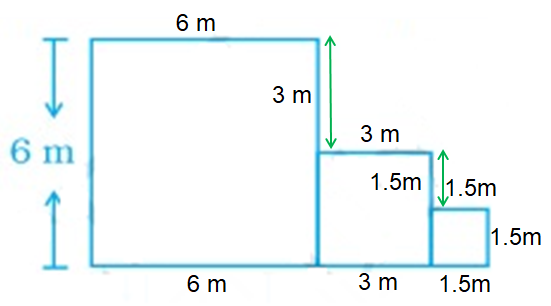
Each square is attached at the mid-point of the side of the square to its right.

So, the side of each adjacent square is half of the previous square.

So, side of 2^nd square is 3 m.

side of 3^rd square is 1.5 m.

Perimeter of the complete figure (going in anticlockwise direction).

= 6 + 6 + 6 + 3 + 1.5 + 1.5 + 1.5 + 1.5 + 3 + 3

Perimeter = 33 m

Problem 7 :

The perimeter of five squares are 24 cm, 32 cm, 76 cm, 40 cm and 80 cm respectively. The perimeter of the another square equal in area of sum of the area of these squares is 

a)  31 cm   b)  62 cm   c)  124 cm     d)  961 cm

Solution :

Perimeter of the first square = 24 cm

Side length of first sqaure = 24/4

= 6 cm

Perimeter of the second square = 32 cm

Side length of second sqaure = 32/4

= 8 cm

Perimeter of the third square = 76 cm

Side length of third sqaure = 76/4

= 19 cm

Perimeter of the fourth square = 40 cm

Side length of fourth sqaure = 40/4

= 10 cm

Perimeter of the fifth square = 80 cm

Side length of fifth sqaure = 80/4

= 20 cm

Perimeter of another square = 6² + 8² + 19² + 10² + 20²

= 36 + 64 + 361 + 100 + 400

= 961 cm