PROBLEMS ON ANGLES OF TRIANGLE

The variable expression represent the angle measures of a triangle. Find the measures of each angle. Then classify the triangle by its angles.

Problem 1 :

∠A = x°, ∠B = 2x°, ∠C = (2x+15)°

Solution :

Sum of angles of a triangle = 180

x + 2x + 2x + 15 = 180

5x + 15 = 180

Subtracting 15 on both sides.

5x = 180 - 15

5x = 165

Divide by 5 on both sides.

x = 165/5

x = 33

Problem 2 :

∠A = x°, ∠B = 7x°, ∠C = x

Solution :

Sum of angles of a triangle = 180

x + 7x + x = 180

9x = 180

Divide by 9 on both sides.

x = 180/9

x = 20

∠A = 20, ∠B = 7(20) ==>  140, ∠C = 20

Problem 3 :

∠A = (x - 15)°, ∠B = (2x - 165)°, ∠C = 90°

Solution :

Sum of angles of a triangle = 180

x - 15 + 2x - 165 + 90 = 180

3x - 180 + 90 = 180

3x - 90 = 180

Add 90 on both sides.

3x = 180 + 90

3x = 270

Divide by 3 on both sides.

x = 270/3

x = 90

Find the measure of the exterior angle shown.

Problem 4 :

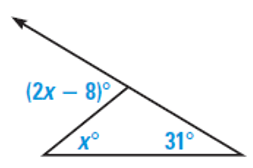
Solution :

Exterior angle = 2x - 8 ---(1)

Remote interior angles are x and 31.

Sum of remote interior angle = Exterior angle

2x - 8 = x + 31

2x - x = 31 + 8

x = 39

Applying the value of x in (1), we get

= 2(39) - 8

= 78 - 8

= 70

So, the required exterior angle is 70.

Problem 5 :

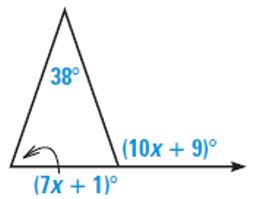
Solution :

Exterior angle = 10x + 9  ------(1)

Remote interior angles are 38 and 7x + 1.

Sum of remote interior angle = Exterior angle

38 + 7x + 1 = 10x + 9

39 + 7x = 10x + 9

Subtract 7x on both sides.

39 = 10x - 7x + 9

39 = 3x + 9

Subtract 9 on both sides.

39 - 9 = 3x 

3x = 30

Dividing by on both sides, we get

x = 30/3

x = 10

Applying the value of x in (1), we get

= 10(10) + 9

= 100 + 9

= 109

So, the required exterior angle is 109.

Problem 6 :

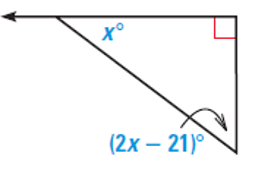
Solution :

The given triangle is right triangle.

Sum of interior angles = 180

x + 2x - 21 + 90 = 180

3x + 69 = 180

Subtracting 69 on both sides.

3x = 180 - 69

3x = 111

Dividing by 3 on both sides.

x = 111/3

x = 37

Exterior angle + x = 180

Exterior angle = 180 - x

Exterior angle = 180 - 37

Exterior angle = 143

Problem 7 :

In triangle PQR, the measure of ∠P is 36. The measure of ∠Q is five times the measure of ∠R. Find ∠Q and ∠R.

Solution :

∠P = 36,∠Q = 5∠R

∠P + ∠Q + ∠R = 180

36 + 5∠R + ∠R = 180

Subtract 36 on both sides.

6∠R = 180 - 36

6∠R = 144

Divide by 6 on both sides.

∠R = 144/6

∠R = 24

∠Q = 5(24) ==>  120

Problem 8 :

The measure of an exterior angle of a triangle is 120. The interior angles that are not adjacent to this exterior angle are congruent. Find the measures of the interior angles of the triangle.

Solution :

Let x be the required angle.

x + x = 120

2x = 120

x = 120/2

x = 60