PROBLEMS ON ALTERNATE ANGLES

Alternate angles :

When two parallel lines are cut by a third line, then angles in alternate positions are equal in size.

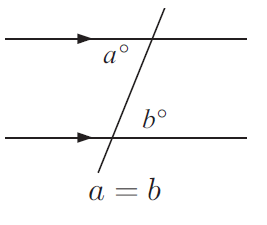
Find the value of unknown of the following :

Problem 1 :

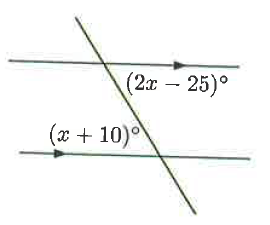
Solution :

Considering the angles marked in the picture given above are in alternate position, they are alternate opposite angles.

x + 10 = 2x - 25

Subtracting 2x on both sides.

x - 2x + 10 = -25

Subtracting 10 on both sides.

-x = -25 - 10

-x = -35

x = 35

Problem 2 :

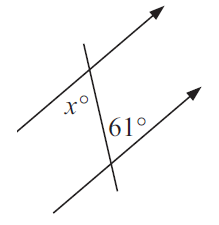
Solution :

x = 61° (Alternate interior angles)

Problem 3 :

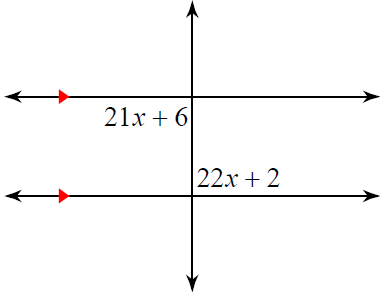
Solution :

21x + 6 and 22x + 2 are alternate interior angles.

21x + 6 = 22x + 2

Subtracting 22x on both sides.

21x - 22x + 6 = 2

Subtracting 6 on both sides.

-x = 2 - 6

x = 4

Problem 4 :

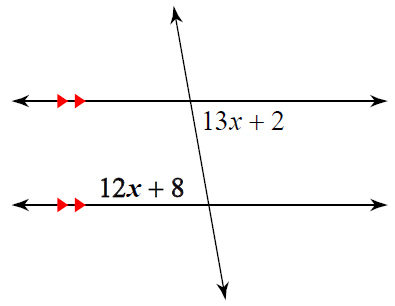
Solution :

12x + 8 and 13x + 2 are alternate interior angles.

12x + 8 = 13x + 2

Subtracting 13x on both sides.

12x - 13x + 8 = 2

Subtracting 8 on both sides.

-x = 2 - 8

x = 6

Problem 5 :

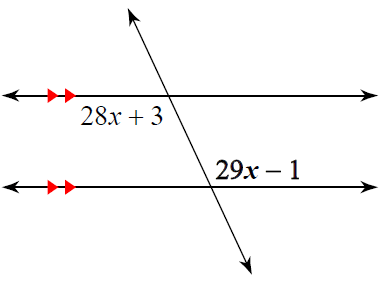
Solution :

28x + 3 and 29x - 1 are alternate interior angles.

28x + 3 = 29x - 1

Subtracting 29x on both sides.

28x - 29x + 3 = -1

Subtracting 3 on both sides.

-x = -1 - 3

x = 4

Problem 6 :

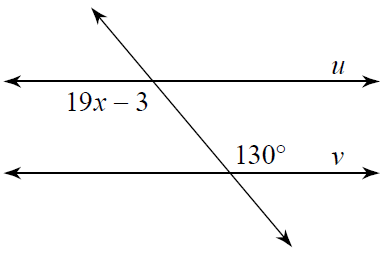
Solution :

19x - 3 and 130 are alternate interior angles.

19x - 3 = 130

Add 3 on both sides.

19x = 130 + 3

19x = 133

Dividing by 19 on both sides.

x = 133/19

x = 7

Problem 7 :

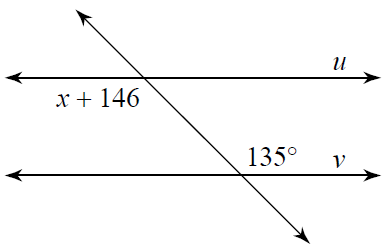
Solution :

x + 146 and 135 are alternate interior angles.

x + 146 = 135

x = 135 - 146

x = -11

Problem 8 :

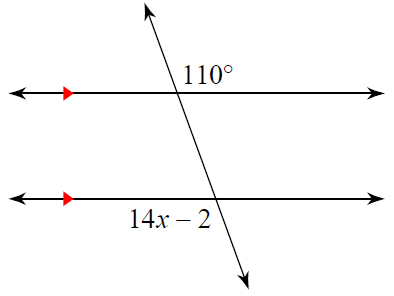
Solution :

14x - 2 and 110 are alternate exterior angles.

14x - 2 = 110

Adding 2 on both sides.

14x = 110 + 2

14x = 112

Dividing by 14 on both sides.

x = 112/14

x = 8

Problem 9 :

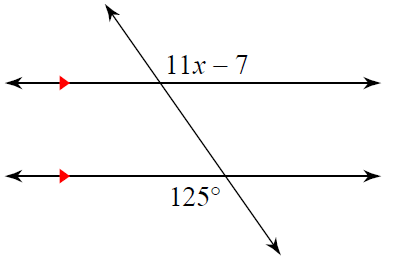
Solution :

11x - 7 and 125 are alternate exterior angles.

11x - 7 = 125

Adding 7 on both sides.

11x = 125 + 7

11x = 132

Dividing by 11 on both sides.

x = 132/11

x = 12

Problem 10 :

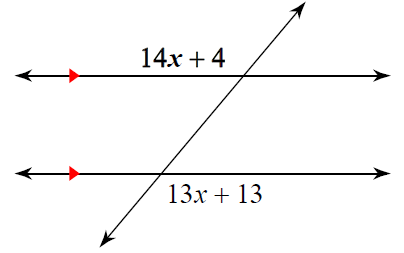
Solution :

14x + 4 and 13x + 13 are alternate exterior angles.

14x + 4 = 13x + 13

Subtracting 13x on both sides.

14x - 13x + 4 = 13

x + 4 = 13

Subtracting 4 on both sides.

x = 13 - 4

x = 9