PROBLEMS ON ADJACENT ANGLES
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Two angles which have same vertex and share a common arm are called adjacent angles.
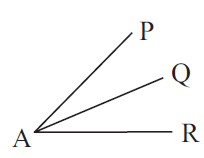
∠PAQ and ∠QAR are adjacent angles.
Adjacent at a point :
The sum of the sizes of the angles at a point is 360 degree
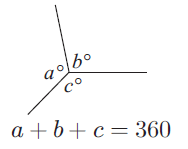
Adjacent angles on a straight line :
The sum of sizes of the angles on a line is 180 degree. The angles are supplementary.
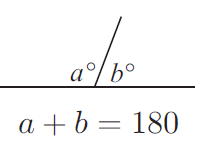
Find the unknown values of the following.
Problem 1 :
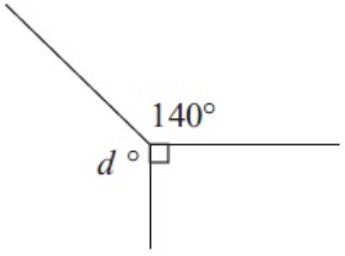
Solution :
90 + d + 140 = 360
230 + d = 360
Subtracting 230, we get
d = 360 - 230
d = 130
Problem 2 :
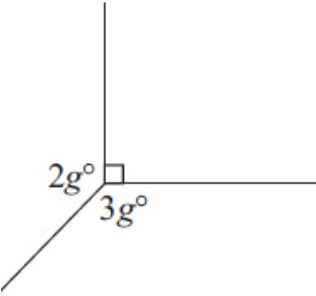
Solution :
2g + 3g + 90 = 360
5g + 90 = 360
5g = 360 - 90
5g = 270
g = 270/5
g = 54
Problem 3 :
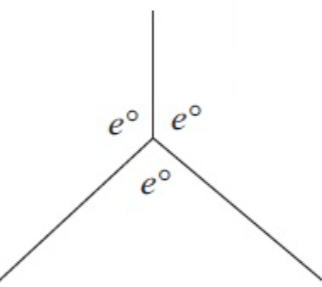
Solution :
e + e + e = 360
3e = 360
Dividing by 3, we get
e = 360/3
e = 120
Problem 4 :
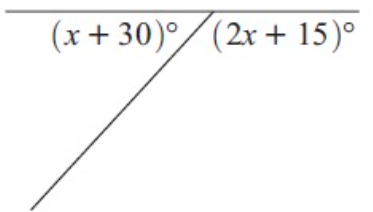
Solution :
x + 30 + 2x + 15 = 180
3x + 45 = 180
3x = 180 - 45
3x = 135
x = 135/3
x = 45
Problem 5 :
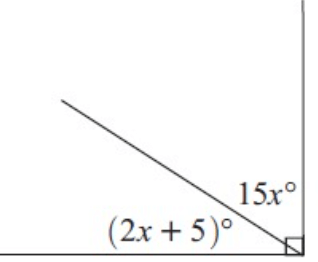
Solution :
2x + 5 + 15x = 90
17x + 5 = 90
Subtracting 5, we get
17x = 90 - 5
17x = 85
Dividing by 17, we get
x = 85/17
x = 5
Problem 6 :
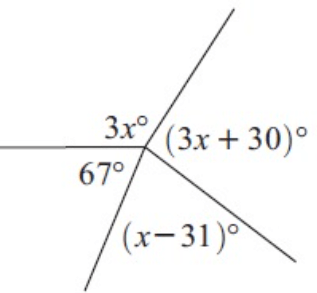
Solution :
3x + 67 + x - 31 + 3x + 30 = 360
7x + 67 + 30 - 31 = 360
7x + 66 = 360
7x = 360 - 66
7x = 294
x = 294/7
x = 42
Problem 7 :
Use the figure shown.
a. Name a pair of adjacent angles.
b. Name a pair of vertical angles.
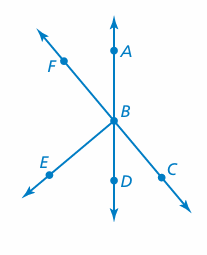
Solution :
a) ∠ABC and ∠ABF share a common side and have the same vertex B. So, ∠ABC and ∠ABF are adjacent angles.
b) ∠ABF and ∠CBD are opposite angles formed by the intersection of two lines. So, ∠ABF and ∠CBD are vertical angles.
Problem 8 :
Name two pairs of adjacent angles and two pairs of vertical angles in the figure.
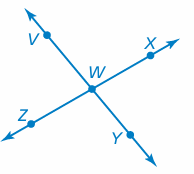
Solution :
Adjacent angles will share the common vertex.
- ∠ZWV and ∠VWX are adjacent angles.
- ∠ZWY and ∠YWX are adjacent angles.
Vertical angles should lie opposite.
- ∠ZWV = ∠XWY are vertical angles
- ∠VWX = ∠ZWY are vertical angles
Problem 9 :
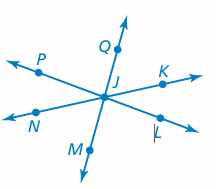
Solution :
Adjacent angles will share the common vertex.
- ∠NJP and ∠PJQ are adjacent angles.
- ∠QJK and ∠KJL are adjacent angles.
- ∠LJM and ∠MJN are adjacent angles.
Vertical angles should lie opposite.
- ∠PJQ = ∠MJL are vertical angles
- ∠NJM = ∠QJK are vertical angles
Problem 10 :
If angles x and y form a linear pair and x – 2y = 30°, then the value of y is
(a) 50° (b) 110° (c) 210° (d) 60°
Solution :
Since x and y are linear pair, the sum of the angles will be equal to 180 degree.
x + y = 180 -----(1)
x - 2y = 30 -----(2)
(1) - (2)
x + y - (x - 2y) = 180 - 30
x + y - x + 2y = 150
3y = 150
y = 150/3
y = 50
Applying the value of y in (1), we get
x + 50 = 180
x = 180 - 50
x = 130
So, option a is correct.
Problem 11 :
In the figure, AB is a straight line, then the value of (a + b) is
(a) 0° (b) 90° (c) 180° (d) 60°
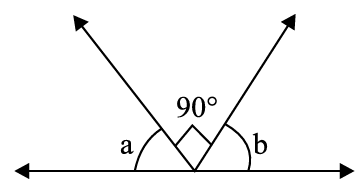
Solution :
Here a and 90 are adjacent angles. b and 90 are adjacent angles
The sum of these angles must be 180 degree. So, a + 90 + b = 180
a + b = 180 - 90
a + b = 90
Problem 12 :
If ∠AOC = 50° then the value of ∠BOD is ________
(a) 50° (b) 40° (c) 130° (d) 25°
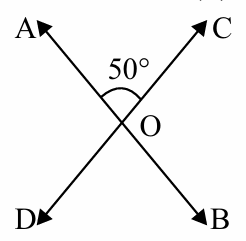
Solution :
- ∠BOC and ∠DOA are vertical angles.
- ∠AOC and ∠DOB are vertical angles.
∠AOC = ∠DOB = 50
So, option a is correct.
Problem 13 :
If two parallel lines are intersected by a transversal, then the interior angles on the same side of transversal are
(a) equal (b) Adjacent (c) supplementary (d) complementary
Solution :
In parallel lines and transversal, the interior angles on the same side of transversal will be co-interior angles and they are supplementary.
Problem 14 :
In figure, l || m value of x is _________
(a) 70° (c) 210° (b) 35° (d) 110°
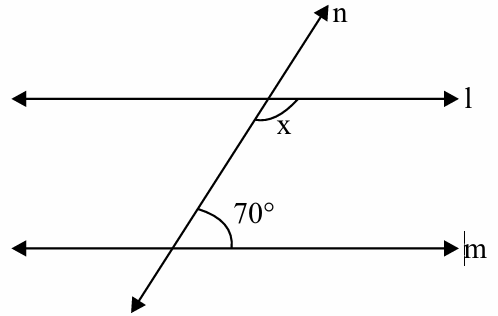
Solution :
70 and x are co-interior angles, and they are supplementary.
70 + x = 180
x = 180 - 70
x = 110
Problem 15 :
Three parallel lines intersect at __________ points
(a) one (b) two (c) three (d) zero
Solution :
Parallel lines will not intersect each other, then there is no point of intersection. Option d is correct.
Problem 16 :
If one angle of a linear pair is acute, then the other angle will be
(a) right angle (b) obtuse angle (c) acute angle (d) straight angle
Solution :
Linear pairs should be add upto 18, then if one angle is acute other angle must be obtuse.
Problem 17 :
In the given figure, find the value of y
(a) 18° (b) 10° (c) 30° (d) 36°
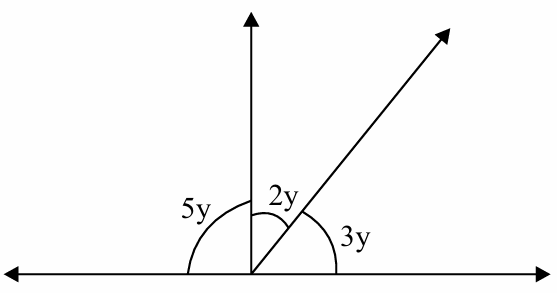
Solution :
5y + 2y + 3y = 180
10y = 180
y = 180/18
y = 10
So, the value of y is 10.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling