PROBLEMS INVOLVING QUADRATIC FUNCTIONS

The equation which is in the form

f(x) = ax² + bx + c

is known as quadratic equation.

The graphical form of quadratic function is parabola. Based on the signs of a, we can say the parabola opens upward or downward.

• If sign of a is +, then the parabola opens upward.
• If sign of a is -, then the parabola opens downward.

Equation of parabola can be converted into three different forms.

• Standard form
• Vertex form
• Factored form.

Problem 1 :

Which of the following gives the solution set for the polynomial equation below?

x²−11𝑥+19 = −5

A. {-3, -8}     B. {3, 8}       C. {-3, 8}      D. {3, -8}

Solution :

x²−11𝑥+19 = −5

Add 5 on both sides.

x²−11𝑥+19+5 = 0

x²−11𝑥+24 = 0

(x - 3) (x - 8) = 0

Equating each factors to zero, we get

x = 3 and x = 8

So, the solution set is {-8, 3}

Problem 2 :

Which of the following could be the equation for the polynomial function below?

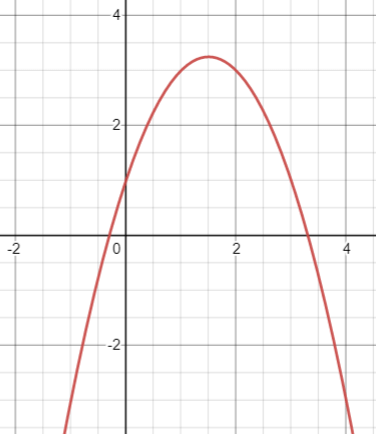
A. y = −x²+3x+1     B. y = x²−0.25x+3.25

C. y = x²−x+3       D. y=−x²+0.25x−3.25

Solution :

From the graph, the parabola opens down. So, we can clearly reject options B and C.

Option (A) :

𝑦 = −x²+3x+1

Converting into vertex form, we get

h = 3/2 and k = 13/4

From the graph, the vertex in between 2 and 4. So, option A is correct.

Problem 3 :

Which of the following is an equation for the function below and gives the coordinates of the vertex as constants or coefficients?

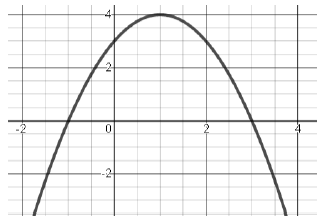
A. y = −(x−3)(x+1)         B. y = −x²+2x+3

C. y = (x+1)²+4             D. y = −(x−1)²+4

Solution :

y = −(x−3)(x+1)

Equating each factor to zero, we get

x = 3 and x = -1

By observing the graph given above, it opens downward and x-intercepts are 3 and -1.

Finding vertex :

y = −(x−3)(x+1)

y = −(x²-3x+1x−3)

y = −(x²-2x−3)

y = −(x² - 2⋅x⋅1 + 1² -1² − 3)

y = −[(x-1)² - 4]

y = −(x-1)² + 4

Vertex is (1, 4).

So, option A is correct.

Problem 4 :

How many solutions are there to the following system of equations?

y = −(1/2)x²+7 and 𝑦 = −2x²+5

A. 0        B. 1       C. 2         D. 3

Solution :

y = −(1/2)x²+7 ------(1) y = −2x²+5  ------(2)

To find the points of intersection, we can solve (1) and (2).

(1) = (2)

−(1/2)x²+7 = −2x²+5 

-x² + 14 = -4x² + 10

3x² = -10 - 14

3x² = -24

x² = -8

x = √-8

It is not real number, so it will not have solution. So, zero solution is the answer.

Problem 5 :

a)  Use x-intercepts to find the axis of symmetry of y = (x + 2)(x - 5)

b)  Check your answer to a. by writing the function in the form y = ax² + bx + c and then evalauting -b/2a.

Solution :

a)

y = (x + 2)(x - 5)

Midpoing of x-intercepts = axis of symmetry

x + 2 = 0 and x - 5 = 0

x = -2 and x = 5

Midpoing of x-intercepts = (-2 + 5)/2

x = 3/2

b)  

y = (x + 2)(x - 5)

y = x² - 5x + 2x - 10

= x² - 3x - 10

Comparing with y = ax² + bx + c, we get a = 1, b = -3 and c = -10

x = -b/2a

x = -(-3)/2(1)

x = 3/2

In both ways, we get the same answer.

Problem 6 :

Let p(x) = a(x + 4)(x - 2) the following diagram shows part of the graph of f.

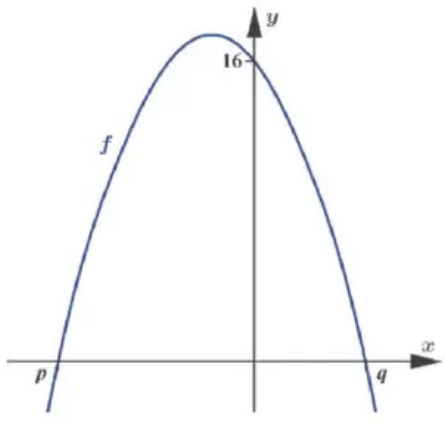
a) Write down the value of p and q.

b)  Show that a = -2

c)  Find the equation of the axis of symmetery of the graph of f.

d)  Locate the axis of symmetry on the graph.

e)  Calculate the maximum value of f.

f)  Write the equation in vertex form.

Solution :

a) Here p and q are x-intercepts.

p(x) = 0

a(x + 4)(x - 2) = 0

x + 4 = 0 and x = -4

x - 2 = 0 and x = 2

the value of p is -4 and q is 2.

b) The parabola passes through (0, 16).

p(x) = a(x + 4)(x - 2)

Applying the point, we get

p(0) = a(0 + 4)(0 - 2)

16 = a(4)(-2)

-8a = 16

a = -2

c)  Equation of axis of symmetery = (-4 + 2)/2

= -2/2

So, the axis of symmetry is x = -1.

d)  At x = -1

e)  y = -2(-1 + 4)(-1 - 2)

y = -2(3)(-3)

y = 18

f)  p(x) = -2(x + 4)(x - 2)

= -2[x² - 2x + 4x - 8]

= -2[x² + 2x - 8]

= -2x² - 4x + 16

-2(x² - 2x + 8)

= -2[(x - 1)² - 1 + 8]

= -2[(x - 1)² + 7]

y = -2(x - 1)² - 14