PROBLEM ON TRIANGLES FOR SAT

Problem 1 :

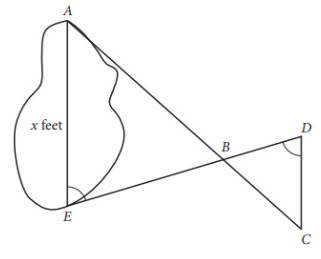
A summer camp counselor wants to find a length, x, in feet, across a lake as represented in the sketch above. The lengths represented by AB, EB, BD and CD on the sketch were determined to be 1800 feet, 1400 feet, 700 feet and 800 feet respectively. Segments AC and DE intersect at B, and ∠AEB and ∠CDB have the same measure. What is the value of x?

Solution:

∠AEB = ∠EDC and

∠ABE =∠DBC

△ABE and △DBC are similar,

Problem 2 :

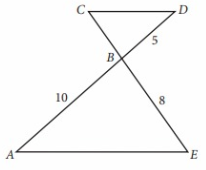
In the figure above, AE || CD and segment AD intersects segments CE at B. What is the length of segment CE?

Solution:

AE || CD and ∠1 = ∠2

∠D = ∠A (Alternate interior angles are equal)

△CDB ~ △EAB

Problem 3 :

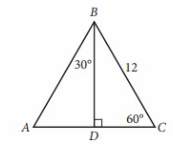
In △ABC above, what is the length of AD?

A) 4      B) 6         C) 6√2          D) 6√3

Solution:

In △BDC, 

∠DBC = 180° - ∠C - ∠BDC

= 180° - 60° - 90°

= 30°

Using special right triangles, 

Side opposite the 90 = 2 x smaller side

DC = smaller side

2(DC) = 12

DC = 6

So, option (B) is correct.

Problem 4 :

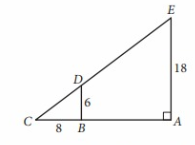
In the figure above, BD is parallel to AE. What is the length of CE?

Solution:

By using Pythagoras theorem,

CD = √(6² + 8²)

= √(36 + 64)

= √100

CD = 10

 △CDB ~  △CEA

Problem 5 :

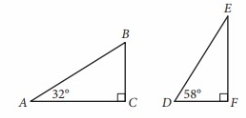
Triangles ABC and DEF are shown above. Which of the following is equal to the ratio BC/AB?

Solution:

= DF/DE

So, option (B) is correct.

Problem 6 :

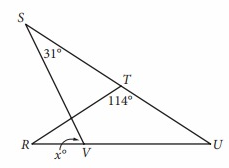
In the figure above, RT = TU. What is the value of x ?

A) 72     B) 66      C) 64      D) 58       

Solution:

As per given as

RT = TU then ∠TUV = ∠TRV

2∠U + 114 = 180°

2∠U = 180 - 114

2∠U = 66

∠U = 66/2

∠U = 33°

∠STR = 180 - 114

= 66

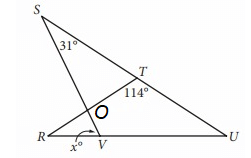
∠SOT = 180 - (31+66)

= 83

Vertically opposite angles will be equal,

∠SOT = ∠ROV = 83

∠ORV + ∠RVO + ∠VOR = 180

33 + x + 83 = 180

x = 180 - (33 + 83)

x = 64

So, option (C) is correct.

Problem 7 :

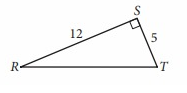
In triangle RST above, point W (not shown) lies on RT. What is the value of cos (∠RSW) - sin(∠WST) ?

Solution:

∠RSW + ∠WST = 90°

cos∠RSW = sin∠WST

cos∠RSW - sin∠WST = 0

Problem 8 :

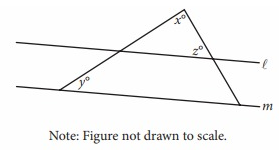
In the figure above, lines l and m are parallel, y = 20, and z = 60. What is the value of x ?

A) 120    B) 100     C) 90     D) 80

Solution:

The sum of all the angles in a triangle add up to 180.

x + y + z = 180

x + 20 + 60 = 180

x + 80 = 180

x = 180 - 80

x = 100

So, option (B) is correct.

Problem 9 :

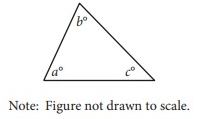
In the triangle above, a = 34. What is the value of b + c?

Solution:

 a + b + c = 180

34 + b + c = 180

b + c = 180 - 34

b + c = 146

So, the value of b + c is 146.