Prime Factorization Method to Find HCF and LCM

Find the HCF of LCM of following numbers using prime factorization method :

Problem 1 :

9, 12

Solution :

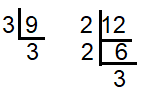
9 = 3 × 3 ==> 3²

12 = 2 x 2 × 3 ==> 2² x 3

HCF of (9, 12) = 3

LCM of (9, 12) = 2² x 3² ==> 36 

Problem 2 :

8, 16

Solution :

8, 16

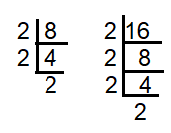
8 = 2 × 2 x 2 ==> 2³

16 = 2 × 2 × 2 x 2 ==> 2⁴

HCF of (8, 16) = 2³ ==> 8

LCM of (8, 16) = 2⁴ ==> 16

Problem 3 :

18, 42

Solution :

18, 42

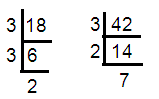
18 = 3 × 3 × 2 ==> 3² x 2

42 =  3 × 2 × 7

HCF of (18, 42) = 3 × 2 ==> 6

LCM of (18, 42) = 3² × 2 x 7 ==> 126

Problem 4 :     

14, 42

Solution :

14, 42

14 = 2 × 7

42 = 2 × 3 × 7

HCF of (14, 42) = 2 × 7 ==> 14

LCM of (14, 42) = 2 × 3 x 7 ==> 42

Problem 5 :

18, 30

Solution :

18, 30

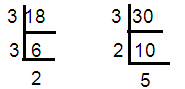
18 = 3 × 3 × 2 ==> 3² x 2

 30 = 3 × 2 × 5

HCF of (18, 30) =  3 × 2 ==> 6

LCM of (18, 30) =  3² × 2 x 5 ==> 90

Problem 6 :

24, 32

Solution :

24, 32

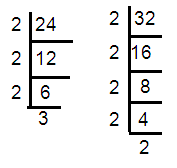
24 =  2 × 2 × 2 × 3 ==> 2³ x 3

32 =  2 × 2 × 2 × 2 × 2 ==> 2⁵

HCF of (24, 32) = 2³ ==> 8

LCM of (24, 32) = 2⁵ x 3 ==> 96

Problem 7 :

12, 36

Solution :

12, 36

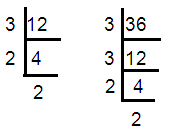
12 = 3 × 2 × 2 ==> 2² x 3

36 = 3 × 3 × 2 × 2 ==> 3² x 2² 

HCF of (12, 36) = 3 × 2² ==> 12

LCM of (12, 36) = 3² × 2²  ==> 36

Problem 8 :

15, 33

Solution :

15, 33

15 = 3 × 5

33 = 3 × 11

HCF of (15, 33) = 3

LCM of (15, 33) = 3 x 11 x 5 ==> 165

Problem 9 :

72, 96

Solution :

72, 96 

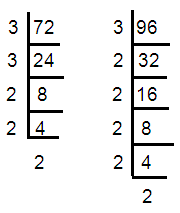
72 = 3 × 3 × 2 × 2 ==> 3² x 2²

96 = 3 × 2 × 2 × 2 × 2 × 2 ==> 3 x 2⁵

HCF of (72, 96) = 3 × 2² ==> 12

LCM of (72, 96) = 3² × 2⁵ ==> 288

Problem 10 :

108, 144

Solution :

108, 144

108 = 2 x 2 x 3 x 3 x 3

= 2² x 3³

144 = 2 x 2 x 2 x 2 x 3 x 3

= 2⁴ x 3²

HCF of (108, 144) = 2² x 3² ==> 36

LCM of (108, 144) = 2⁴ x 3³ ==>  432

Problem 11 :

78, 130

Solution :

78, 130

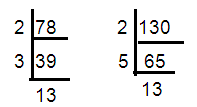
78 = 2 × 3 x 13

130 = 2 × 5 x 13

HCF of (78, 130) ==> 26

LCM of (78, 130) = 2 x 5 x 3 x13 ==> 390

Problem 12 :

The brass section of a marching band has 30 members. The band director arranges the brass section in rows. Each row has the same number of members. How many possible arrangements are there?

Solution :

Use the factor pairs of 30 to fi nd the number of arrangements.

• 30 = 1 ⋅ 30   (There could be 1 row of 30 or 30 rows of 1)
• 30 = 2 ⋅ 15  (There could be 2 rows of 15 or 15 rows of 2) 
• 30 = 3 ⋅ 10 (There could be 3 rows of 10 or 10 rows of 3)
• 30 = 5 ⋅ 6  (There could be 5 rows of 6 or 6 rows of 5)
• 30 = 6 ⋅ 5 (The factors 5 and 6 are already listed)

There are 8 possible arrangements:

1 row of 30, 30 rows of 1, 2 rows of 15, 15 rows of 2, 3 rows of 10, 10 rows of 3, 5 rows of 6, or 6 rows of 5.

Problem 13 :

You are filling piñatas for your sister’s birthday party. The list shows the gifts you are putting into the piñatas. You want identical groups of gifts in each piñata with no gifts left over. What is the greatest number of piñatas you can make?

Solution :

The GCF of the numbers of gifts represents the greatest number of identical groups of gifts you can make with no gifts left over. So, to find the number of piñatas, fi nd the GCF.

18 = 2 ⋅ 3 ⋅ 3

24 = 2 ⋅ 3 ⋅ 2 ⋅ 2

42 = 2 ⋅ 3 ⋅ 7

2 ⋅ 3 = 6

Find the product of the common prime factors. The GCF of 18, 24, and 42 is 6. So, you can make at most 6 piñatas.