PRACTICE PROBLEMS ON TYPES OF DISCONTINUITY
State whether or not each of the following functions is continuous.
- If not, state where the discontinuity occurs and whether or not it is removable.
- Is the discontinuity is an asymptote, a hole or jump ?
- If an asymptote, what is its equation ?
Problem 1 :
Problem 2 :
Problem 3 :
Problem 4 :
Problem 5 :
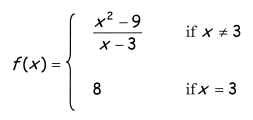
Problem 6 :
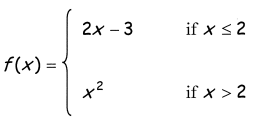
Problem 7 :
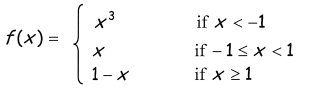
Problem 8 :
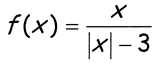
Problem 9 :
Find the value of a if the function is continuous.
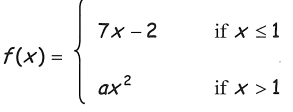
Problem 10 :
Find the value of a if the function is continuous.
Problem 11 :
Answer Key
1)
The function is discontinuous at x = -1/2 and 1.
Type of discontinuity = Non removable
Vertical asymptotes are at x = -1/2 and x = 1.
2)
The function is discontinuous at x = -1/2 and 1.
Type of discontinuity = Non removable
Vertical asymptotes are at x = -1/2 and x = 1.
3)
The function is discontinuous at x = 3 and -2.
Type of discontinuity = Non removable
Vertical asymptotes are at x = 3 and x = -2.
4)
So, the vertical asymptote is at x = -4
Hole is at x = 4. When x = 4, y = 1/5
5) The function is not continuous at x = 3, there is removable discontinuity at (3, 6).
6) Since Lim x->2- f(x) = Lim x->2+ f(x), then lim x ->2 f(x) does not exists.
Type of discontinuity = Jump discontinuity
7)
At x = 1, the function is not continuous, then the limit does not exists.
There is jump discontinuity at x = 1.
8) f(x) is not continuous at x = 3 and x = -3, there is vertical asymptote at x = 3 and x = -3
9) a = 5
10) a = 4/3
11) a = 4 and b = -2
Recent Articles
-
Finding Range of Values Inequality Problems
May 21, 24 08:51 PM
Finding Range of Values Inequality Problems -
Solving Two Step Inequality Word Problems
May 21, 24 08:51 AM
Solving Two Step Inequality Word Problems -
Exponential Function Context and Data Modeling
May 20, 24 10:45 PM
Exponential Function Context and Data Modeling