PRACTICE PROBLEMS ON QUADRATIC EQUATION FOR CA FOUNDATION

Problem 1 :

Solving equation x² - (a + b)x + ab = 0, we find the value(s) of x ?

(a)  a      (b)  b   (c) a, b    (d)  None of these

Solution

Problem 2 :

Solving the equation z + √z = 6/25, then the value of z.

(a)  1/5      (b)  2/5     (c) 1/25      (d)  2/25

Solution

Problem 3 :

If

(x + 2)/(x - 2) - (x - 2)/(x + 2) = (x - 1)/(x + 3) - (x + 3)/(x - 3)

then the value of x are 

(a)  0, ±√6      (b)   0, ±√3     (c)  0, ±2√3       (d)  None

Solution

Problem 4 :

 Solve (x - 1/x)² + 2(x + 1/x) = 7 1/4

Solution

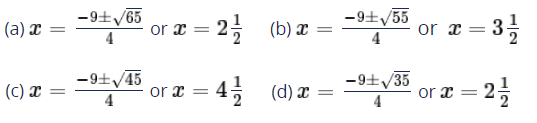
Problem 5 :

The solution of the equation x - √(25 - x²) = 1

(a)  x = -3     (b)  x =  ±5     (c)  x = 1      (d)  x = 4

Solution

Problem 6 :

Solve the equation 

(6x + 2)/4 + (2x² - 1)/(2x² + 2) = (10x - 1)/4x we get roots as

(a)  x = -1     (b)  x =  ±1     (c)  x = 1      (d)  x = 0

Solution

Problem 7 :

If α and β  are the roots of

x² = x + 1

then the value of α²/β - β²/α is

(a)  2√5      (b)  √5     (c)  3√5      (d)  -2√5

Solution

Problem 8 :

Solving x² + y² - 25 = 0 and x - y - 1 = 0, we get the roots 

(a)  ±3, ±4     (b)  ±2, ±3     (c)  0, 3,  4      (d)  0, -3, -4

Solution

Problem 9 :

The roots of a ax² + bx + c = 0, are real and unequal if

(a) b²< 4ac     (b) b² = 4ac   (c) b² > 4ac    (d) None

Solution

Problem 10 :

α, β are the roots of the equation x² - 5x + 6 = 0 the equation with the roots (α β + α + β) and (α β - α - β) is 

(a) x² - 12x + 11 = 0    (b) 2x² - 6x + 12 = 0

(c) x² - 12x - 12 = 0    (d) None

Solution

Problem 11 :

If p ≠ q and p² = 5p - 3 and q² = 5q - 3 the equation having roots as p/q and q/p is

(a) x² - 19x + 3 = 0    (b) 3x² - 19x - 3 = 0

(c) 3x² - 19x + 3 = 0    (d) 3x² + 19x + 3 = 0

Solution

Problem 12 :

Two numbers are such that thrice the smaller number exceeds twice the greater one by 18 and 1/3 of the smaller and 1/5 of the greater number are together 21. The numbers are -

(a) (45,36)     (b) (50, 38)      (c) (54,45)       (d) (55,41)

Solution

Problem 13 :

Two sides of an equilateral triangle are shortened by 12 units 13 units and 14 units respectively and a right angle is formed. The sides of the equilateral triangle is 

(a) 17 units      (b) 16 units      (c) 15 units      (d) 18 units

Solution

Problem 14 :

The hypotenuse of a right-angled triangle is 20 cm. The difference between its other two sides is 4cm. The sides are

(a) (11cm, 15cm)       (b) (12cm, 16cm)

(c) (20cm, 24cm)       (d) None of these

Solution

Problem 15 :

The sum of two numbers is 45 and the mean proportional between them is 18. The numbers are

(a) (15, 30)     (b) (32, 13)     (c) (36, 9)        (d) (25, 20)

Solution

Problem 16 :

Solving the equation 7√(x/(1-x) + 8√(1-x)/x = 15

(a) 64/113, 1/2       (b) 1/50, 1/65

(c) 49/50, 1/65      (d) 1/50, 64/65

Solution

Problem 17 :

Solving x³ + 9x² - x - 9 = 0 we get the following roots

(a) ± 1,-9     (b) ±1, ±9      (c) ±1, 9      (d) None

Solution

Problem 18 :

The solution of the cubic equation x³ - 6x² + 11 x - 6 = 0 is given by the triplet

(a) (-1, 1, -2)    (b) (1, 2, 3)      (c) (-2, 2, 3)     (d) (0, 4, -5)

Solution

Find the values of k for which the given quadratic equations have real and equal roots.

Problem 1 :

4x² + kx + 9 = 0

Solution

Problem 2 :

kx² - 5x + k = 0

Solution

Problem 3 :

x² - 7(3+k) + 4 - 2x(1 + k) = 0

Solution

Problem 4 :

Consider x² - 2x + m = 0. Find the discriminant, hence find the values of m for which the equation has

a) repeated roots

b) 2 distinct real roots

c)  no real roots

Solution

Problem 5 :

If -4 is a root of the quadratic equation x² + px - 4 = 0 and the quadratic equation 12x² + 4px + k = 0 has equal roots, the find the value of k.

Solution

Problem 6 :

If the equation (1+k²)x² + 2kqx + (q² - p²) = 0 has equal roots, then shown that q² = p²(1 + k²).

Solution