PRACTICE PROBLEMS ON PROPERTIES OF QUADRILATERALS

Problem 1 :

Solve the following problems:

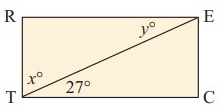
a. RECT is a rectangle. Find the values of x and y.

Solution:

Property used :

In diagonals all angles will be 90 degree.

∠CTR = 90°

∠CTR = ∠CTE + ∠ETR

90° = 27° + x

x = 63°

In a rectangle, opposite sides are parallel and equal. Then alternate interior angles are equal. So, y = 27

Problem 2 :

PARM is a parallelogram. Find the size of:

i. PMR     ii. ARM     iii. PAR   

Solution:

Property used :

In parallelogram, opposite sides are parallel, then sum of co-interior angles will be 180 degree.

∠APM = ∠ARM = 67° (opposite angles are equal)

∠APM and ∠PMR are co-interior angles.

∠PMR = 180° - ∠APM

∠PMR = 180° - 67°

∠PMR = 113°

∠PMR = ∠PAR = 113° (opposite angles are equal)

So, PMR = 113°

ARM = 67°

PAR = 113°

Problem 3 :

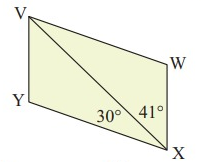
VWXY is a parallelogram. Find the size of:

i.WVX     ii. YVX     iii. VYX     iv. VWX

Solution :

Property used :

In parallelogram, opposite sides are parallel, then alternate interior angles are equal.

Since it is a parallelogram, opposite sides will be parallel.

i. ∠WVX = ∠YXV = 30° (Alternate angles are congruent)

ii. ∠YVX = ∠VXW = 41° (Alternate angles are congruent)

iii. ∠VYX = 180° - (30° + 41°)

∠VYX = 180° - 71°

∠VYX = 109°

iv.  ∠VWX = 180° - (30° + 41°)

∠VWX = 180° - 71°

∠VWX = 109°

Problem 4 :

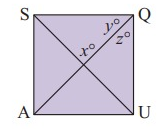
SQUA is a square. Find the values of:

i. x     ii. y     iii. z

Solution:

Property used :

The diagonal will intersect each other at 90 degree and the diagonals will bisect the angle at vertex.

∠A = ∠S = ∠Q = ∠U = 90°

∠SQU = 90°

x = 180° - 90°

x = 90°

Diagonals will bisect the angles at vertices

y = 45°

z = 45°

Use the information given to name the quadrilateral and find the values of the variables:

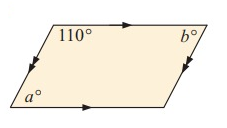
Problem 5 :

Solution:

Property used :

In parallelogram, the opposite sides are parallel and sum of co-interior angles will be 180 degree.

It is parallelogram.

a = b (opposite angles are equal)

180 ° = a + 110 °

a = 180° - 110 °

a = 70° and b = 70°

Problem 6 :

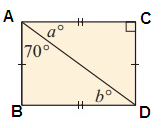
Solution:

Property used :

In a rectangle, each vertices will have angle measure of 90 degree.

∠CAD + ∠ADC = 90°

a = b

∠BAD + ∠DAC = 90

70 + a = 90

a = 90 - 70

a = 20

Alternate interior angles are equal, then

b = 20°

Problem 7 :

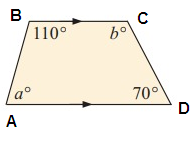
Solution:

Property used :

In a trapezium, since the the opposite sides are parallel co-interior angles add upto 180.

∠BAD + ∠ABC = 180° (co interior angles)

a + 110° = 180°

a = 180° - 110°

a = 70°

∠ADC + ∠BCD = 180°

70° + b = 180°

b = 180° - 70°

b = 110°

Problem 8 :

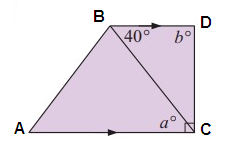
Solution:

Property used :

In a trapezium, since the the opposite sides are parallel co-interior angles add upto 180.

∠CBD = ∠ACB

40° = a

∠ACD = 90°

∠BDC + ∠ACD = 180°

b + 90° = 180°

b = 90°

Problem 9 :

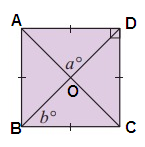
Solution:

Property used :

In a square the diagonals will intersect each other at 90 degree.

∠A = ∠B = ∠C = ∠D = 90°

Diagonals will be perpendicular.

a = 90°

Diagonals will bisect the angles at vertices.

b = 45°

Problem 10 :

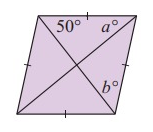
Solution :

Property used :

In rhombus diagonals will be perpendicular.

50° + a + 90 = 180°

50° + a = 180° - 90

a = 90° - 50°

a = 40°

40° + b = 90°

b = 90° - 40°

b = 50°

Problem 11 :

PQRS is a rectangle. Find the values of:

a. a     b. b     c. c

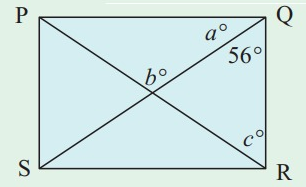
Solution:

Property used :

In a rectangle, the vertices will have 90 degree and diagonals will be perpendicular.

56° + a = 90°

a = 90° - 56°

a = 34°

b = 90°

90° + 56° + c = 180°

c = 180° - 146°

c = 34°

Problem 12 :

Using the information given on the diagram, name the figure and find the values of x and y.

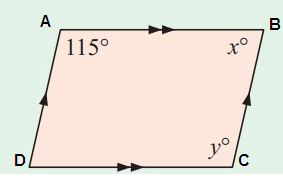
Solution:

Property used :

In rhombus, since the sides are parallel sum of co-interior angles add upto 180.

∠A = 115° and ∠C = 115°

∠B = 180° - 115°

∠B = 65°

So, x = 65°

y = 115° 

Problem 13 :

PQRS is a rhombus. Find the values of x and y.

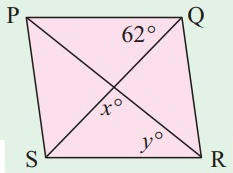
Solution:

Property used :

In parallelogram, the diagonals will intersect each other at 90 degree angle measure.

PQ ∥ SR

∠QSR = 62°

x = 90

90° + 62° + y = 180°

152° + y = 180°

y = 180° - 152°

y = 28°