PRACTICE PROBLEMS ON DIVIDING POLYNIMIALS FOR SAT

Problem 1:

The equation

is true for all values of x ≠ 2/3, where k is a constant. What is the value of k?

a.8     b.9     c.11     d.15

Solution :

= (5x + 8) - 4 / (3x - 2)

= (5x + 8) (3x - 2) - 4 / (3x - 2)

= (15x² - 10x + 24x - 16 - 4) / (3x - 2)

= (15x² +14x - 20) / (3x - 2)

(kx² + 14x - 20) / (3x - 2) = (15x² +14x - 20) / (3x - 2)

k = 15

The value of k is 15.

So, option (d) is correct.

Problem 2 :

The expression

(3x² + 4) / (x + 1)

is equivalent to which of the following?

a. (3x - 3) + 1 / (x + 1)          b. (3x - 3) + 7 / (x + 1)

c. (3x + 3) + 1 / (x + 1)         d. (3x + 3) + 7 / (x + 1)

Solution :

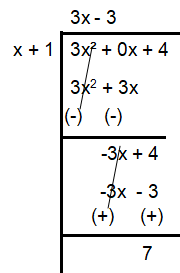
Writing the above in the form of

Quotient + (Remainder / Divisor)

we get,

(3x - 3) + 7/(x + 1)

So, option (b) is correct.

Problem 3 :

x³ - 3x² + 3x - 9 = 0

For what real value of x is the equation above true?

Solution :

x³ - 3x² + 3x - 9 = 0

(x³ - 3x²) + (3x - 9) = 0

x²(x - 3) + 3(x - 3) = 0

(x - 3) (x² + 3) = 0

x - 3 = 0 or x² + 3 = 0

x = 3

So, the value of x is 3.

Problem 4 :

What is the remainder when x² + 2x + 1 is divided by x + 3?

Solution :

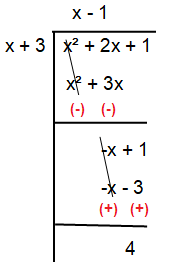
Remainder = 4

Using the concept remainder theorem, we can find the remainder.

Let p(x) = x² + 2x + 1

x + 3 = 0

x = -3

p(-3) = (-3)² + 2(-3) + 1

= 9 - 6 + 1

= 10 - 6

= 4

Problem 5 :

When 3x² + x + 2 is divided by x - 1, the result can be expresses as

(ax + b) + c/(x - 1)

where a, b and c are constants. What is the value of a + b + c?

Solution :

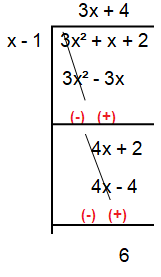
3x² + x + 2) / (x - 1) = (3x + 4) + 6 / (x - 1)

Now comparing with

= (ax + b) + c / (x - 1)

Here a = 3, b = 4, c = 6

a + b + c = 3 + 4 + 6

= 13

So, the value of a + b + c is 13.

Problem 6 :

When 2x² - 5x + 3 is divided by 2x + 1, the result can be written as (x - 3) + R / (2x + 1), where R is a constant. What is the value of R?

Solution :

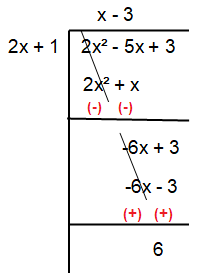
= (x - 3) + 6 / (2x + 1)

So, the value of R is 6.

Problem 7:

p(x) = (3x² - 5) (x + k) - 20

In the polynomial p(x) defined above, k is a constant. If x is a factor of p(x), what is the value of k?

a.-6     b.-4     c.2     d.4

Solution:

p(x) = (3x² - 5) (x + k) - 20

= 3x³ + 3kx² - 5x - 5k - 20

= x (3x² + 3kx - 5) - 5k - 20

If x is a factor,

Then -5k - 20 = 0

-5k = 20

k = -4

So, option (b) is correct.

Problem 8:

In the xy-plane, how many times does the graph of

f(x) = (x - 3) (x - 1) (x + 2)²

intersect the x-axis?

a.2     b.3     c.4     d.5

Solution :

f(x) = (x - 3) (x - 1) (x + 2)²

(x - 3) (x - 1) (x + 2)² = 0

x - 3 = 0 or x - 1 = 0 or (x + 2)² = 0

x = 3 or x = 1 or x = -2

The curve is intersecting the graph 3 times with multiplicity of  -2 as 2.