PRACTICE PROBLEMS ON COLLINEAR POINTS

Points A, B and C are collinear. Point B is between A and C. Find the length indicated.

Problem 1 :

Find AC if AB = 16 and BC = 12.

Solution :

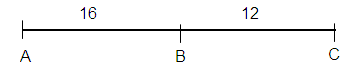
AC = AB + BC

AC = 16 + 12

AC = 28

Problem 2 :

Find AC if AB = 13 and BC = 9.

Solution :

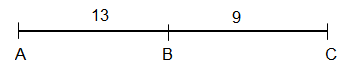
AC = AB + BC

AC = 13 + 9

AC = 22

Points A, B and C are collinear. Point B is between A and C. Solve for x.

Problem 3 :

AC = 3x + 3, AB = -1 + 2x, and BC = 11. Find x.

Solution :

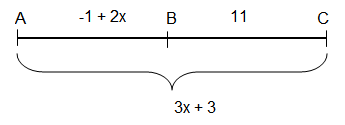
AC = AB + BC

3x + 3 = -1 + 2x + 11

3x + 3 = 10 + 2x

3x - 2x = 10 - 3

x = 7

So, the value of x is 7.

Problem 4 :

AC = 22, BC = x + 14, and AB = x + 10. Find x.

Solution :

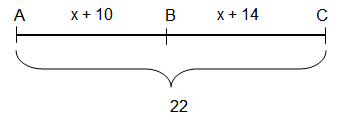
AC = AB + BC

22 = x + 10 + x + 14

22 = 2x + 24

22 - 24 = 2x

-2 = 2x

x = -2/2

x = -1

So, the value of x is -1.

Solve for x :

Problem 5 :

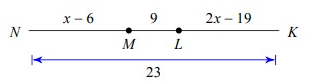
Solution :

By observing the figure. 

NK = NM + ML + LK

23 = x - 6 + 9 + 2x - 19

23 = 3x - 16

3x = 23 + 16

3x = 39

x = 39/3

x = 13

So, the value of x is 13.

Solve for x :

Problem 6 :

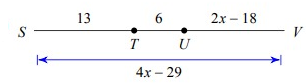
Solution :

By observing the figure. 

SV = ST + TU + UV

4x - 29 = 13 + 6 + 2x - 18

4x - 29 = 1 + 2x

4x - 2x = 1 + 29

2x = 30

x = 30/2

x = 15

So, the value of x is 15.

Problem 7 :

Points A, B, C, D and E are collinear and in that order. Find AC if AE = x + 50 and CE = x + 32.

Solution : 

A, B, C, D and E are collinear.

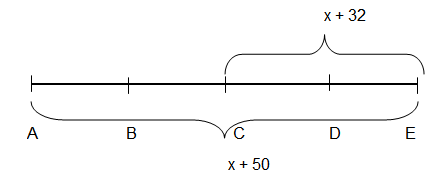
To find AC :

AE = x + 50

CE = x + 32

AC = AE - CE

AC = x + 50 - x + 32

AC = 18

So, the value of AC is 18.