PRACTICE ON ARITHMETIC SEQUENCE AND SERIES

Problem 1 :

Which term of the AP

3/√7, 4/√7, 5/√7, ............ is 17/√7 ?

Solution :

3/√7, 4/√7, 5/√7, ............ is 17/√7

Let general term be 17/√7.

t_n = 17/√7, a = 3/√7 and d = 4/√7 - 3/√7 ==>  1/√7

a + (n - 1)d  = 17/√7

3/√7 + (n - 1)(1/√7)  = 17/√7

(n - 1)(1/√7)  = 17/√7 - 3/√7

(n - 1)(1/√7)  = 17/√7 - 3/√7

(n - 1)(1/√7)  = 14/√7

n - 1 = (14/√7) √7

n - 1 = 14

n = 15

So, 15th term of the arithmetic series is 17/√7.

Problem 2 :

Divide 69 into three parts which are in A.P and are such that the product of the first two parts is 483.

Solution :

Let the first three terms be a - d, a and a + d.

Sum of three terms = 69

a - d + a + a + d = 69

3a = 69

a = 23

Product of three terms = 483

a (a - d) = 483

23(23 - d) = 483

(23 - d) = 483/23

23 - d = 21

d = 23 - 21

d = 2

a - d ==>  23 - 2 ==> 21

a = 23

a + d ==>  23 + 2 ==>  25

So, the required terms are 21, 23 and 25.

Problem 3 :

Insert 4 arithmetic means between 4 and 324.

Solution :

let b, c, d and e are those 4 required terms.

4, b, c, d, e, 324.

First term (a) = 4

6^th term = 324

t₆ = 324

a + 5d = 324 ----(1)

By applying the value of a in (1), we get 

4 + 5d = 324

5d = 324 - 4

5d = 320

d = 320/5

d = 64

Problem 4 :

If the p^th term of an A.P is q and q^th term is p the value of the r^th term is 

(a)  p - q - r     (b) p + q - r    (c) p + q + r    (d)  None

Solution :

t_p = a + (p - 1)d = q ----(1)

t_q = a + (q - 1)d = p----(2)

(1) - (2)

[a + (p - 1)d] - [a + (q - 1)d] = q - p

d(p - 1 - q + 1) = q - p

d(p - q) = q - p

d = -1

By applying the value of d in (1), we get

a + (p-1) (-1) = q

a = q + p - 1

r^th term :

t_r = a + (r - 1) d

t_r = q + p - 1 + (r - 1) (-1)

t_r = q + p - 1 - r + 1

t_r = q + p - r

Problem 5 :

The sum of a series in A.P is 72 the first term is 17 and the common difference -2, the number of terms is 

(a)  6     (b)  12     (c)  6 or 12     (d) None

Solution :

s_n = 72, a = 17 and d = -2

s_n = (n/2)[2a+ (n - 1) d]

72 = (n/2)[2(17)+ (n - 1) (-2)]

72 = (n/2)[34 - 2n + 2]

72 = (n/2)[36 - 2n]

72 = n[18 - n]

18n - n² = 72

n2 - 18n + 72 = 0

(n - 12)(n - 6) = 0

n = 6 and n = 12

Problem 6 :

The sum of all natural numbers between 500 and 1000, which are divisible by 13 is

(a)  28400     (b)  28405     (c)  28410     (d) None

Solution :

To find the first number which is divisible by 13 and more than 500 is 507.

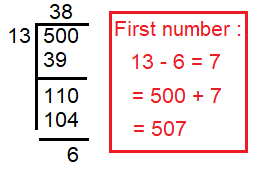
To find the last number which is divisible by 13 and lesser than 1000 is 988.

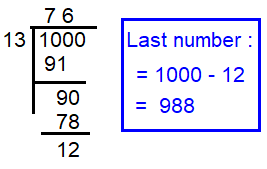
507 + 520 + 533 + .................+ 988

Number of terms between 507 to 988 are 

n = [(l-a)/d] + 1

n = [(988 - 507) / 13] + 1

n = 38

Sum of 38 terms :

s₃₈ = (38/2)[507 + 988]

s₃₈ = 19[1495]

s₃₈ = 28405

So, the sum of numbers between 500 to 1000 which are divisible by 13 is 28405.

Problem 7 :

If the 10^th term of an A.P. is twice the 4^th term, and the 23^rd term is 'k' times the 8^th term, then the value of 'k' is

(a) 2.5      (b) 3        (c) 3.5        (d) 4

Solution :

10^th term = 2(4^th term)  ----(1)

23^rd term = k(8^th term) ----(2)

From (1)

a + 9d = 2(a + 3d)

2a - a + 6d - 9d = 0

a - 3d = 0

a = 3d

From (2)

a + 22d = k(a + 7d)

Applying the value of a, we get

3d + 22d = k(3d + 7d)

25d = k(10d)

25/10 = k

k = 2.5

Problem 8 :

The sum of the A.M. and G.M. of two positive numbers is equal to the difference between the numbers. The numbers are in the ratio.

(a) 1 : 3       (b) 1 : 6       (c) 9 : 1        (d) 1 : 12

Solution :

Let a, c and b be three terms.

Arithmetic mean = (a + b)/2

Geometric mean = √ab

(a + b)/2 + √ab = a - b

√ab = (a - b) - [(a + b)/2]

√ab = (2a - 2b - a - b)/2

√ab = (a - 3b)/2

Taking squares on both sides.

4ab = a² - 6ab + b²

a² - 4ab - 6ab + 9b² = 0

a² - 10ab + 9b² = 0

a² - ab - 9ab + 9b² = 0

a(a - b) -9b(a - b) = 0

(a - b) (a - 9b) = 0

a = 9b

a/b = 9 : 1

So, the answer is 9 : 1.