POPULATION GROWTH AND DECAY WORD PROBLEMS WORKSHEET

Write an exponential function to model each situation. Find each amount at the end of the specified time. Round your answers to the nearest whole number.

Problem 1 :

A town with a population of 5,000 grows 3% per year. Find the population at the end of 10 years.

Solution

Problem 2 :

The population of Boomtown is 475,000 and is increasing at a rate of 3.75% each year. When will the population exceed 1 million people (to the nearest year)?        Solution

Problem 3 :

The population of Leave town is 123,000 and is decreasing at a rate of 2.375% each year.

• When will the population of Leave town drop below 50,000 (to the nearest year)?

• What will the population of Leave town be 100 years from now?

Solution

Problem 4 :

Problem The 1989 population of Mexico was estimated at 87,000,000. The annual growth rate is 2.4%. When will the population reach 100,000,000 (to the nearest year)?

Solution

Problem 5 :

The population of Small town in the year 1890 was 6,250. Since then, it has increased at a rate of 3.75% each year.

a) What was the population of Small town in the year 1915?

a) In 1940?

c) What will the population of Small town be in the year 2003?

d) When will the population reach 1,000,000 (to the nearest year)?                    Solution

Problem 6 :

You have a checking account and a money market account at a local bank. Your checking account has a constant balance of $200. The table shows the total balance of the accounts over time.

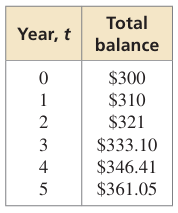
a. Write a function m that represents the balance of your money market account after t years.

b. Write a function B that represents the total balance after t years. Compare the graph of m to the graph of B.

 Solution

Answer Key

1)  y = 6720

2)  it will take 21 years tp reach the population of 1 million.

3) i)   it will take 38 years.

ii)  y = 11118

4)  the population will become 100,000,000 after 6 years.

5)  a)  y = 15688

b)  at 1914 the population will be 39380.

c)  y = 400438.

d)  After 147 years, the population will be 1,000,000.

6)  a) 100(1 + 0.1)^t

b)  100(1.1)^t+ 200

Problem 1 :

You deposit $500 into a savings account that earns 6% interest each year and you do not make any deposits or withdrawals.

1) What is the initial amount?

2) Write an equation to model this situation. Use 𝑦 for the total value of the account and 𝑡 for the number of years.

3) What is the growth factor?

4) What is the value of this account in 25 years?

Solution

Problem 2 :

You are given a car worth $9500 on your 16th birthday. The value of the car declines by 15% per year.

1) What is the initial amount?

2) Write an equation to model this situation. Use 𝑦 for the total value of the car and 𝑡 for the number of years after your 16th birthday.

3) What is the decay factor?

4) What is the value of the car in 5 years? Round to two decimal places, as needed

Solution

Problem 3 :

A new sports car sells for $35,000. The value of the car decreases by 18% annually.

a)  Which of the following choices models the yearly value of the car since its purchase?

b)  Find the decay factor ?

a)  y = 35000(1.18)^x      b)  y = 35000(0.82)^x

c)  y = 35000(0.18)^x      b)  y = 35000(-0.18)^x

Solution

Problem 4 :

At the end of last year, the population of Jason’s hometown was approximately 75,000 people. The population is growing at the rate of 2.4% each year. Which equation models the growth?

a)  y = 75000(1.24)^x      b)  y = 75000(1.024)^x

c)  y = 75000(0.76)^x      b)  y = 75000(0.976)^x

Solution

Problem 5 :

Select which exponential function below models this situation: Lupe bought a gold chain for $350, and the value of the chain increases by 4% per year. Use 𝑦 for the value of the chain and 𝑡 for the time in years

a) 𝑦 = 350^4x            b) 𝑦 = 350(4)^x

c) 𝑦 = 350(1.4)^x         d) 𝑦 = 350(1.04)^x

Solution

Problem 6 :

Sam buys a car for $55,000. The value of the car depreciates at a rate of 15% per year.

a) What is the initial value?

b) Write an exponential function to model the value of the car (𝑦) after 𝑡 years.

c) What is the decay factor?

d) Find the value of the car after 4 years.

Solution