POLYNOMIAL FUNCTIONS AND THEIR GRAPHS SAT

Problem 1 :

If -1 and 1 are two real roots of the polynomial function 

f(x) = ax³ + bx² + cx + d

and (0, 3) is the y-intercept of graph f, what is the value of b ?

a)  -3    b)  -1    c)  2      d)  4

Solution :

Since -1 and 1 are real roots of the polynomial function, 

f(1) = 0 and f(-1) = 0

f(x) = ax³ + bx² + cx + d

f(1) = a(1)³ + b(1)² + c(1) + d

a + b + c + d = 0 -----(1)

f(-1) = a(-1)³ + b(-1)² + c(-1) + d

-a + b - c + d = 0 -----(2)

Since (0, 3) is one of the points of the polynomial, we get

3 = a(0)³ + b(0)² + c(0) + d

3 = d

(1) + (2)

a + b + c + d + (-a + b - c + d) = 0

2b + 2d = 0

b + d = 0 -----(3)

Applying the value of d in (3), we get

b + 3 = 0

b = -3

So, the value of b is -3.

Problem 2 :

What is the remainder of the polynomial

p(x) = 81x⁵ - 121x³ - 36

is divided by x + 1 ?

Solution :

x + 1 = 0

x = -1

p(x) = 81x⁵ - 121x³ - 36

p(-1) = 81(-1)⁵ - 121(-1)³ - 36

p(-1) = -81 + 121 - 36

= 121 - 117

= 4

So, the remainder is 4.

Problem 3 :

If x - 2 is a factor of polynomial

p(x) = a(x³ - 2x) + b(x² - 5)

Which of the following must be true ?

a) a + b = 0    b)  2a - b = 0    c)  2a + b = 0   d)  4a - b = 0

Solution :

p(x) = a(x³ - 2x) + b(x² - 5)

Since x - 2 is a factor, then p(2) = 0

p(2) = a(2³ - 2(2)) + b(2² - 5)

0 = a(8 - 4) + b(4 - 5)

0 = 4a + b(-1)

4a - b = 0

So, option d is correct.

Problem 4 :

The function f is defined of the polynomial. Some values of x and f(x) are shown in the table above. Which of the following must be a factor of f(x) ?

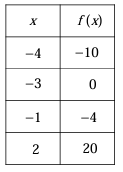
Solution :

If a is a factor of the polynomial f(x), then f(x - a) will be 0. By observing the table, when x = -3, f(-3) = 0.

-3 is a solution for the polynomial f(x). By converting into factor, we will get x + 3.

Problem 5 :

x³ - 8x² + 3x - 24 = 0

For what real of x is the equation above true ?

Solution :

x³ - 8x² + 3x - 24 = 0

By grouping method,

x² (x - 8) + 3(x - 8) = 0

By factoring (x - 8), we get

(x² + 3)(x - 8) = 0

Equating each factor to 0, we get 

x² = -3 and x = 8

Here 8 is the real solution.

Problem 6 :

If x > 0, what is the solution of the equation

x⁴ - 8x² = 9 ?

Solution :

x⁴ - 8x² = 9

x²(x² - 8) = 0

Equating each factor to 0, we get

x² = 0 and  x² - 8 = 0

x = 0 and x² = 8

x = √8

x = ± 2√2

Since the value of x is greater than 0, then x = 2√2.

Problem 7 :

If the graph of

f(x) = 2x³ + bx² + 4x - 4

intersects the x-axis at (1/2, 0) and (-2, k) lies on the graph of f. What is the value of k ?

a)  -4     b)  -2      c)  0       d)  2

Solution :

f(x) = 2x³ + bx² + 4x - 4

Since the curve intersects the x-axis at 1/2,

f(1/2) = 2(1/2)³ + b(1/2)² + 4(1/2) - 4

0 = 1/4 + b/4 + 2 - 4

0 = [ (1 + b) / 4 ] - 2

(1 + b) / 4 = 2

1 + b = 8

b = 8 - 1

b = 7

Applying the value of b, we get

f(x) = 2x³ + 7x² + 4x - 4

(-2, k) lies on the graph of f(x), applying x = -2 and y = k

k = 2(-2)³ + 7(-2)² + 4(-2) - 4

k = -16 + 28 - 8 - 4

k = -28 + 28

k = 0

So, the value of k is 0.

Problem 8 :

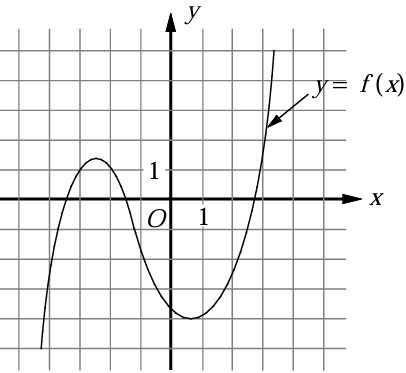
The function y = f(x) is graphed on the xy- plane above. If k is a constant such that the equation f(x) = k has one real solution, which of the following could be the value of k?

a)  -3      b)  -1     c)  1      d)  3

Solution :

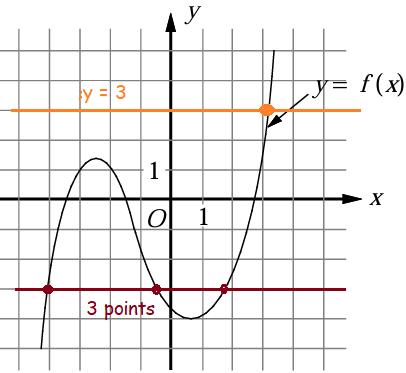
Drawing the horizontal lines, the line y = 3 is intersecting the curve at 1 point. That is, it has one real solution. then option d is correct.