PERIOD AMPLITUDE AND EQUATION OF AXIS FROM THE TABLE

State the period, amplitude, and equation of the axis of the trigonometric function that produces each of the following tables of values. Then use this information to write the equation of the function

Problem 1 :

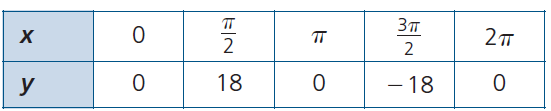
Solution :

The points are (0, 0) (π/2, 18) (π, 0) (3π/2, -18) and (2π, 0)

Since the initial position is (0, 0), it must be a sin function. The maximum value is 18 and minimum is -18.

Amplitude = 18

Period = 2π

Equation of axis is y = 0

Parent function will be 

f(x) = a sin (k(x - d)) + c

a = 18, period = 2π/|k|

2π = 2π/|k|

|k| = 2π/2π

k = 1

Since there is no phase shift, then d = 0

c = 0

f(x) = 18 sin (1(x - 0)) + 0

f(x) = 18 sin x

Problem 2 :

Solution :

The points are (0, -2) (π, 4) (2π, -2) (3π, -8) and (4π, -2)

Since the initial position is (0, -2), it must be a cosine function. The maximum value is 4 and minimum is -8.

Amplitude = -2 - (-8)

= -2 + 8

a = 6

Period = 4π

Equation of axis is y = -2

Parent function will be 

f(x) = a cos (k(x - d)) + c

a = 6, period = 2π/|k|

4π = 2π/|k|

|k| = 2π/4π

k = 1/2

Since there is no phase shift, then d = 0

c = -2

f(x) = 6 cos (1/2 (x)) - 2 

f(x) = 6 cos (x/2) - 2 

Problem 3 :

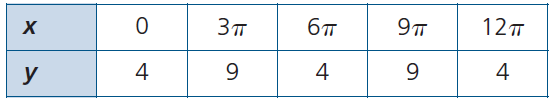
Solution :

The points are (0, 4) (3π, 9) (6π, 4) (9π, 9) and (12π, 4)

Since the initial position is (0, 4), it must be a cosine function. 

Amplitude = (9 - 4)/2

= 5/2

a = 2.5

Period = 6π

Equation of axis is y = (9 + 4)/2

= 13/2

= 6.5

Parent function will be 

f(x) = a cos (k(x - d)) + c

a = 2.5, period = 2π/|k|

6π = 2π/|k|

|k| = 2π/6π

k = 1/3

Since there is no phase shift, then d = 0

c = 6.5

f(x) = -2.5 cos (1/3 (x)) + 6.5

f(x) = -2.5 cos (x/3) + 6.5

Problem 4 :

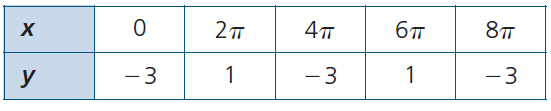
Solution :

The points are (0, -3) (2π, 1) (4π, -3) (6π, 1) and (8π, -3)

Since the initial position is (0, -3), it must be a cosine function. 

Amplitude = (1 - (-3))/2

= (1 + 3)/2

= 4/2

a = 2

Period = 4π

Equation of axis is y = (1 + (-3))/2

= -2/2

= -1

Parent function will be 

f(x) = a sin (k(x - d)) + c

a = 2, period = 2π/|k|

4π = 2π/|k|

|k| = 2π/4π

k = 1/2

Since there is no phase shift, then d = 0

c = -1

f(x) = 2 sin (1/2 (x)) - 1

Problem 5 :

The graph of a sinusoidal function has been horizontally compressed and horizontally translated to the left. It has maximums at the points (-5π/7, 1) and (-3π/7, 1) and it has a minimum at (-4π/7, -1). If the axis in radians, what is the period of the function ?

Solution :

Maximum points are (-5π/7, 1) and (-3π/7, 1)

Minimum at (-4π/7, -1)

Horizontal distance = |-5π/7 + (-3π/7)|

= |(-5π + 3π)/7|

= |-2π/7|

= 2π/7

Amplitude = 2π/7

So, the required period in radians is 2π/7.

Problem 6 :

The graph of a sinusoidal function has been vertically stretched, vertically translated up, and horizontally translated to the right. The graph has a maximum at (π/13, 13) and the equation of the axis is y = 9. If the x-axis is in radians, list one point where the graph has a minimum

Solution :

Height of the graph = (13 - 9) ==> 4

y-coordinate of minimum value = 5

The problem specifies that the graph has been vertically stretched, vertically translated, and horizontally translated to the right, but it does not mention a horizontal stretch or compression. Therefore, the period P of the function remains the standard 2π radians.

In any sinusoidal function, the horizontal distance between a maximum and the consecutive minimum is exactly half of the period:

Period = 2 π/2

= π

The graph has a maximum at x = π/13. To find the -coordinate of a minimum, we add half the period to the x-coordinate of the maximum

= π/13 + π

= 14π/13