PERIMETER OF RHOMBUS

Find the perimeter of each rhombus.

Problem 1 :

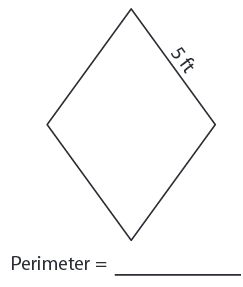
Solution :

Given, side length = 5 ft

Perimeter of the rhombus = 4s

= 4 × 5

= 20 ft

So, perimeter of the rhombus is 20 ft.

Problem 2 :

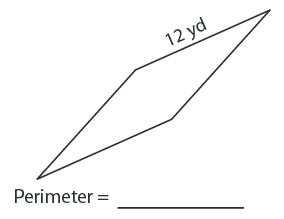
Solution :

Given, side length = 12 yd

Perimeter of the rhombus = 4s

= 4 × 12

= 48 yd

So, perimeter of the rhombus is 48 yd.

Problem 3 :

Solution :

Given, side length = 10 in

Perimeter of the rhombus = 4s

= 4 × 10

= 40 in

So, perimeter of the rhombus is 40 in.

Problem 4 :

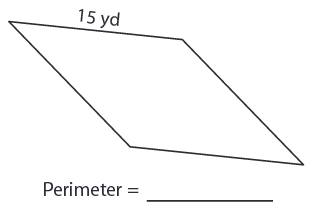
Solution :

Given, side length = 15 yd

Perimeter of the rhombus = 4s

= 4 × 15

= 60 yd

So, perimeter of the rhombus is 60 yd.

Problem 5 :

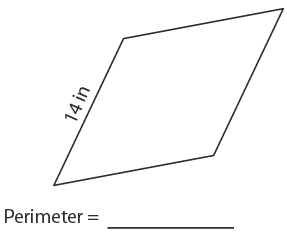
Solution :

Given, side length = 14 in

Perimeter of the rhombus = 4s

= 4 × 14

= 56 in

So, perimeter of the rhombus is 56 in.

Problem 6 :

Solution :

Side length = 4 ft

Perimeter of the rhombus = 4a

= 4 × 4

= 16 ft

So, perimeter of the rhombus is 16 ft.

Problem 7 :

Find the perimeter of the rhombus, if its side is 18 feet long.

Solution :

Side length = 18 ft

Perimeter of the rhombus = 4s

= 4 × 18

= 72 ft

So, perimeter of the rhombus is 72 ft.

Problem 8 :

Determine the perimeter of the rhombus whose side length is 9 yards.

Solution :

Side length = 9 yd

Perimeter of the rhombus = 4s

= 4 × 9

= 36 yd

So, perimeter of the rhombus is 36 yd.

Problem 9 :

The diagonals of a rhombus are 6 cm and 8 cm respectively. Find the length of the sides of the rhombus. Also find its perimeter.

Solution :

In rhombus the diagonals bisect each other and they are perpendicular.

Angle between two diagonals is 90 degree.

Let diagonals be d₁ and d₂

d₁ = 6 cm and d₂ = 8 cm

d₁/2 = 3 cm and d₂/2 = 4 cm

(Side)² = (d₁/2)² + (d₂/2)²

= 3² + 4²

= 9 + 16

(Side)² = 25

side = √25

= 5 cm

So, the side length of the square is 5 cm.

Problem 10 :

The area of rhombus is 150 cm². The length of one of its diagonals is 10 cm. The length of the other diagonal is :

a)  25 cm   b) 30 cm   c)  35 cm   d)  40 cm

Solution :

The area of rhombus = 150 cm².

Length of one diagonal = 10 cm

Let x be the length of other diagonal.

(1/2) • 10 • x = 150

5 • x = 150

x = 150/5

x = 30

So, the length of the other diagonal is 30 cm, option b is correct.

Problem 11 :

One of the diagonals of a rhombus us double the other diagonal. Its area is 25 square cm. The sum of the diagonals is :

a)  10 cm    b)  12 cm   c)  15 cm   d)  16 cm

Solution :

Let diagonals be d₁ and d₂

d₁ = 2d₂

(1/2) • d₁ • d₂ = 25

(1/2) • 2d₂ • d₂ = 25

d₂2 = 25

d₂ = √25

d₂ = 5

d₁ = 2(5)

= 10

Sum of the diagonals = 10 + 5

= 15 cm

Option c is correct.

Problem 12 :

The perimeter of the rhombus is 56 m and its height is 5 m. Its area is 

a) 64 sq.m    b)  70 sq.m    c)  78 sq.m    d 84 sq.m

Solution :

Perimeter of the rhombus = 56 m

4(side length) = 56

side length = 56/4

= 14

height = 5 m

Area of rhombus = base x height

= 14 x 5

= 70 square cm

Option b is correct.

Problem 13 :

If the diagonals of the rhombus are 24 cm and 10 cm, the area and the perimeter of the rhombus are 

a) 120 cm², 52 cm    b)  120 cm², 64 cm     c) 240 cm², 52 cm    d)  240 cm², 64 cm 

Solution :

Let diagonals be d₁ and d₂

d₁ = 24 cm and d₂ = 10 cm

d₁/2 = 12 cm and d₂/2 = 5 cm

(Side)² = (d₁/2)² + (d₁/2)²

= 12² + 5²

= 144 + 25

(Side)² = 169

side = √169

= 13 cm

Area of rhombus = (1/2) • d₁ • d₂ 

= (1/2) • 24 • 10 

= 240/2

= 120 square cm

Perimeter of rhombus = 4(side length)

= 4(13)

= 52 cm

So, the required area is 120 sq.cm and perimeter is 52 cm. Then option a is correct.

Problem 14 :

The perimeter of the rhombus is 40 cm. If one of the diagonal is 8 cm, then what is the area of  the rhombus ?

Solution :

Perimeter of rhombus = 40 cm

Side length of rhombus = 40/4

= 10 cm

d₁ = 8 cm and d₂ = ?

d₁/2 = 4 cm and d₂/2 = ?

(Side)² = (d₁/2)² + (d₂/2)²

10² = 4² + (d₂/2)²

100 = 16 + (d₂/2)²

100 - 16 = (d₂/2)²

(d₂/2)² = 84

d₂/2 = √84

 = 2√21

d₂ = 4√21

Area of rhombus = (1/2) • d₁ • d₂ 

= (1/2) • 8 • 4√21

= 16√21 square cm