PERIMETER OF 2D SHAPES

Find the perimeter of the following:

Problem 1 :

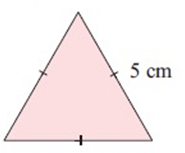
Solution :

Given, side a = 5 cm

Perimeter of a triangle = 3a

= 3 × 5

= 15 cm

So, perimeter of a triangle is 15 cm.

Problem 2 :

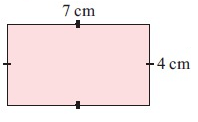
Solution :

Given, length l = 4 cm and width = 7 cm

Perimeter of a rectangle = 2(l + w)

= 2(4 + 7)

= 2(11)

= 22 cm

So, perimeter of a rectangle is 22 cm.

Problem 3 :

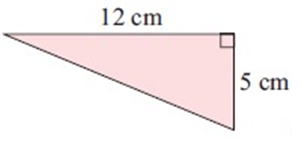
Solution :

Given, a = 5 cm, b = 12 cm

By using Pythagorean Theorem,

c² = a² + b²

c = √(a² + b²)

c = √(5² + 12²)

c = √(25 + 144)

c = √169

c = 13 cm

Perimeter of a triangle = a + b + c

= 5 + 12 + 13

= 30 cm

So, perimeter of a triangle is 30 cm.

Problem 4 :

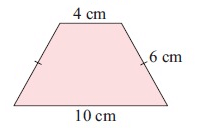
Solution :

Let a = 6 cm, b = 4 cm, c = 6 cm and d = 10 cm

Perimeter of a Trapezoid = a + b + c + d

= 6 + 4 + 6 + 10

= 26 cm

So, Perimeter of a Trapezoid is 26 cm.

Problem 5 :

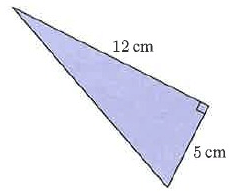
Solution :

Let a = 5 cm, b = 12 cm

By using Pythagorean Theorem,

c² = a² + b²

c = √ (a² + b²)

c = √(5² + 12²)

c = √(25 + 144)

c = √169

c = 13 cm

Perimeter of a triangle = a + b + c

= 5 + 12 + 13

= 30 cm

So, perimeter of a triangle is 30 cm.

Problem 6 :

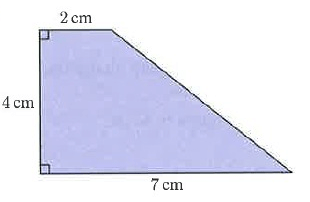
Solution :

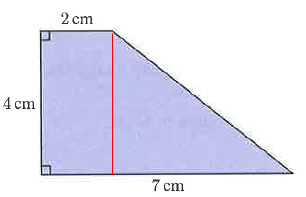
Let a = 4 cm, b = 5 cm

By using Pythagorean Theorem,

c² = a² + b²

c = √(a² + b²)

c = √(4² + 5²)

c = √(16 + 25)

c = √41

c = 6.4 cm

Perimeter of shapes = a + b + c + d

= 4 + 2 + 7 + 6.4

= 19.4 cm

So, perimeter of shapes is 19.4 cm.

Problem 7 :

Kim decides to get fit by running laps of a nearby shopping complex. Its dimensions are shown in the diagram alongside.

How many laps does he have to complete to run 13 km in total?

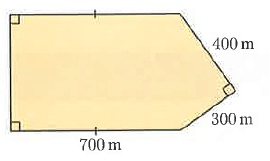
Solution :

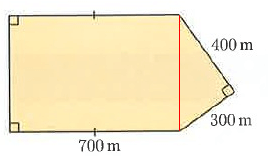
Let a = 400 m and b = 300 m

By using Pythagorean Theorem,

c² = a² + b²

c = √a² + b²

c = √400² + 300²

c = √160000 + 90000

c = √250000

c = 500 m

Perimeter of shapes = 700 + 700 + 500 + 400 + 300

= 2600 m

1 km = 1000 m

13 km = 13000 m

= 13000/2600

= 5 laps

Problem 8 :

A rectangular field measured 290 m by 210 m. How long will it take for a girl to go two times round the field, if she walks at the rate of 1.5 m/s ?

Solution :

Length of rectangle = 290 m and width = 210 m

Perimeter of the field = 2(290 + 210)

= 2(500)

= 1000 m

Distance covered when a girl go two times round the field = 2(1000)

= 2000 m

Time = distance / speed

Speed = 1.5 m/s

Time = 2000/1.5

= 1333.33

To converting into minutes, we have to divide by 60

= 1333.33/60

= 22.22 

So, she will take approximately 22 minutes.

Problem 9 :

A wire is in the shape of a rectangle whose length is 40 cm and breadth is 22 cm .If same wire is bent in the shape of square ,what will be the measure of each side ? Also find which shape encloses more area.

Solution :

Length of rectangle = 40 cm

Width of the rectangle = 22 cm

Perimeter of the rectangle = 2(length + width)

= 2(40 + 22)

= 2(62)

= 124 cm

Perimeter of rectangle = perimeter of square

124 = 4(side length of square)

Side length of square = 124/4

= 31

Area of rectangle = 40 x 22

= 880 square cm

Area of square = 31 x 31

= 961 square cm

So, the shape square covers more area.

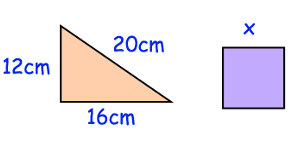
Problem 10 :

The triangle and square have the same perimeter. Find x

Solution :

Perimeter of the right triangle = 12 + 16 + 20

= 48 cm

Perimeter of square = 48

4(side length) = 48

4x = 48

x = 48/4

x = 12 cm

So, the side length of the square is 12 cm.

Problem 11 :

An isosceles triangle has a perimeter of 73cm.

An equilateral triangle has a perimeter of 51cm

The triangles are put together to make a kite.

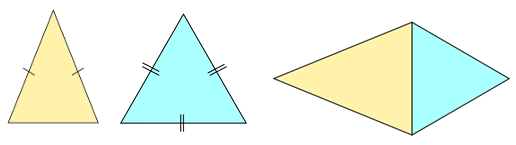
Workout the perimeter of the kite.

Solution :

By observing the kite, it is clear that one side of the isosceles triangle is overlapping one of the sides of the equilateral triangle.

Perimeter of equilateral triangle = 51 cm

Let a be the side length of the equilateral triangle.

3a = 51

a = 51/3

a = 17 cm

Perimeter of the isosceles triangle = 73

Let x be the two equal sides and one known side has the measure of 17 cm.

2x + 17 = 73

2x = 73 - 17

2x = 56

x = 56/2

x = 28

Perimeter of the kite = 56 + 51

= 107 cm